
分析 多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加,据此求出算式(20an-2bn-14an-1bn+1+8a2nb)÷(-2an-3b)的值是多少即可.
解答 解:(20an-2bn-14an-1bn+1+8a2nb)÷(-2an-3b)
=20an-2bn÷(-2an-3b)-14an-1bn+1÷(-2an-3b)+8a2nb÷(-2an-3b)
=-10abn-1+7a2bn-4an+3
故答案为:-10abn-1+7a2bn-4an+3.
点评 此题主要考查了整式的除法,解答此题的关键是熟练掌握整式的除法法则:(1)单项式除以单项式,把系数,同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同他的指数一起作为商的一个因式.(2)多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
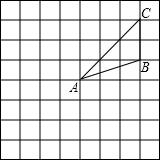 如图所示,在边长为1的网格中,△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.
如图所示,在边长为1的网格中,△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一个直角三角形纸片的锐角顶点A在∠MCN的边OM上移动,移动过程中始终有AB⊥ON于点B,AC⊥OM于点A,∠MON的平分线OP分别交AB,AC于点D、E.
如图,一个直角三角形纸片的锐角顶点A在∠MCN的边OM上移动,移动过程中始终有AB⊥ON于点B,AC⊥OM于点A,∠MON的平分线OP分别交AB,AC于点D、E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | P=Q | B. | P<Q | C. | P>Q | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com