练习册

  • 练习册
  • 试题
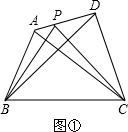
    精英家教网 > 初中数学 > 题目详情

    提出问题：如图1，在四边形ABCD中，P是AD 边上任意一点，△PBC与△ABC和△DBC的面积之间有什 么关系？
    探究发现：为了解决这个问题，我们可以先从一些简单的、特殊的情形人手：

    （1）当AP=AD时（如图2）：
    ∵AP=AD，△ABP和△ABD的高相等，
    ∴S△ABP=
    ∵PD=AD-AP=，
    △CDP和△CDA的高相等，
    ∴S△CDP=，
    ∴S△PBC=


    ；
    （2）当AP=AD时，探求S△PBC与S△ABC和S△DBC之间的关系，写出求解过程；
    （3）当AP=AD时，S△PBC与S△ABC和S△DBC之间的关系式为：______；
    （4）一般地，当AP=AD（n表示正整数）时，探求S△PBC与S△ABC和S△DBC之间的关系，写出求解过程；
    问题解决：当AP=时，S△PBC与S△ABC和S△DBC之间的关系式为：________。
    解：（2）∵AP=AD，△ABP和△ABD的高相等，
    ∴S△ABP=，
    又∵PD=AD-AP=AD，△CDP和△CDA的高相等，
    ∴S△CDP=，
    ∴ S△PBC=S四边形ABCD-S△ABP-S△CDP
    =S四边形ABCD-S△ABD-S△CDA
    =S四边形ABCD-（S四边形ABCD-S△DBC）-（S四边形ABCD-S△ABC）
    =S△DBC+S△ABC
    ∴S△PBC=S△DBC+S△ABC；
    （3）S△PBC=S△DBC+S△ABC；
    （4）S△PBC=S△DBC+S△ABC；
    ∵AP=AD，△ABP和△ABD的高相等，
    ∴S△ABP=S△ABD
     又∵PD=AD-AP=AD，△CDP和△CDA的高相等，
    ∴S△CDP=S△CDA，
    ∴S△PBC=S四边形ABCD-S△ABP-S△CDP
    =S四边形ABCD-S△ABD-S△CDA
    =S四边形ABCD-（S四边形ABCD-S△DBC）-（S四边形ABCD-S△ABC）
    =S△DBC+S△ABC，
    ∴S△PBC=S△DBC+S△ABC
    问题解决：S△PBC=S△DBC+S△ABC。
    练习册系列答案
  • 名校课堂系列答案
  • 西城学科专项测试系列答案
  • 小考必做系列答案
  • 小考实战系列答案
  • 小考复习精要系列答案
  • 小考总动员系列答案
  • 小升初必备冲刺48天系列答案
  • 68所名校图书小升初高分夺冠真卷系列答案
  • 伴你成长周周练月月测系列答案
  • 小升初金卷导练系列答案
    • 年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    阅读下列材料，解答相应问题：
    已知△ABC是等边三角形，AD是高，设AD=h．点P（不与点A、B、C重合）到AB的距离PE=h1，到AC的距离PF=h2，到BC的距离PH=h3．
    如图1，当点P与点D重合时，我们容易发现：h1=
    1
    2
    h，h2=
    1
    2
    h，因此得到：h1+h2=h．
    小明同学大胆猜想提出问题：如图2，若点P在BC边上，但不与点D重合，结论h1+h2=h还成立吗？通过证明，他得到了肯定的答案．证明如下：
    证明：如图3，连接AP．
    ∴S△ABC=S△ABP+S△APC．
    设等边三角形的边长AB=BC=CA=a．
    ∵AD⊥BC，PE⊥AB，PF⊥AC，
    ∴
    1
    2
    BC•AD=
    1
    2
    AB•PE+
    1
    2
    AC•PF
    ∴
    1
    2
    a•h=
    1
    2
    a•h1+
    1
    2
    a•h2．
    ∴h1+h2=h．
    （1）进一步猜想：当点P在BC的延长线上，上述结论还成立吗？若成立，请你证明；若不成立，请猜想h1，h2与 h之间的数量关系，并证明．（借助答题卡上的图4）
    （2）我们容易知道，当点P在CB的延长线及直线AB，AC上时，情况与前述类似，这里不再说明．
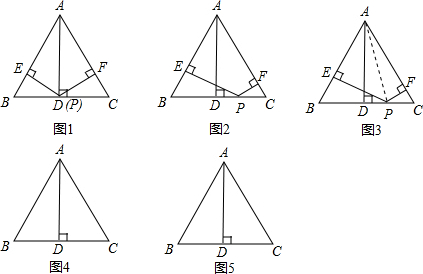    继续猜想，你会进一步提出怎样的问题呢？请在答题卡上借助图5精英家教网画出示意图，写出你提出的问题，并直接写出结论，不必证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    提出问题：如图①，在四边形ABCD中，P是AD边上任意一点，△PBC与△ABC和△DBC的面积之间有什么关系？精英家教网
    探究发现：为了解决这个问题，我们可以先从一些简单的、特殊的情形入手：
    （1）当AP=
    1
    2
    AD时（如图②）：
    精英家教网
    ∵AP=
    1
    2
    AD，△ABP和△ABD的高相等，
    ∴S△ABP=
    1
    2
    S△ABD．
    ∵PD=AD-AP=
    1
    2
    AD，△CDP和△CDA的高相等，
    ∴S△CDP=
    1
    2
    S△CDA．
    ∴S△PBC=S四边形ABCD-S△ABP-S△CDP
    =S四边形ABCD-
    1
    2
    S△ABD-
    1
    2
    S△CDA
    =S四边形ABCD-
    1
    2
    （S四边形ABCD-S△DBC）-
    1
    2
    （S四边形ABCD-S△ABC）
    =
    1
    2
    S△DBC+
    1
    2
    S△ABC．
    （2）当AP=
    1
    3
    AD时，探求S△PBC与S△ABC和S△DBC之间的关系，写出求解过程；
    （3）当AP=
    1
    6
    AD时，S△PBC与S△ABC和S△DBC之间的关系式为：
     
    ；
    （4）一般地，当AP=
    1
    n
    AD（n表示正整数）时，探求S△PBC与S△ABC和S△DBC之间的关系，写出求解过程；
    问题解决：当AP=
    m
    n
    AD（0≤
    m
    n
    ≤1）时，S△PBC与S△ABC和S△DBC之间的关系式为：
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    提出问题：如图，在“儿童节”前夕，小明和小华分别获得一块分布均匀且形状为等腰梯形和直角梯形的蛋糕（AD∥BC），在蛋糕的边缘均匀分布着巧克力，小明和小华决定只切一刀将自己的这块蛋糕平分（要求分得的蛋糕和巧克力质量都一样）．
    精英家教网
    背景介绍：这条分割直线既平分了梯形的面积，又平分了梯形的周长，我们称这条线为梯形的“等分积周线”．
    尝试解决：（1）小明很快就想到了一条分割直线，而且用尺规作图作出．请你帮小明在图1中作出这条“等分积周线”，从而平分蛋糕．
    （2）小华觉得小明的方法很好，所以模仿着在自己的蛋糕（图2）中画了一条直线EF分别交AD、BC于点E、F．你觉得小华会成功吗？如能成功，说出确定的方法；如不能成功，请说明理由．
    （3）通过上面的实践，你一定有了更深刻的认识．若图2中AD∥BC，∠A=90°，AD＜BC，AB=4cm，BC=6cm，CD=5cm．请你找出梯形ABCD的所有“等分积周线”，并简要的说明确定的方法．

    查看答案和解析>>

    科目：初中数学 来源：2013年浙江省衢州市高级中等学校招生考试数学 题型：044

    提出问题

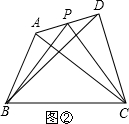
    (1)如图1，在等边△ABC中，点M是BC上的任意一点(不含端点B、C)，连结AM，以AM为边作等边△AMN，连结CN．求证：∠ABC＝∠ACN．

    类比探究

    (2)如图2，在等边△ABC中，点M是BC延长线上的任意一点(不含端点C)，其它条件不变，(1)中结论∠ABC＝∠ACN还成立吗？请说明理由．

    拓展延伸

    (3)如图3，在等腰△ABC中，BA＝BC，点M是BC上的任意一点(不含端点B、C)，连结AM，以AM为边作等腰△AMN，使顶角∠AMN＝∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系，并说明理由．

    查看答案和解析>>

    同步练习册答案