
如图,抛物线y=ax2+bx﹣3a(a≠0)与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,2),连接BC.
(1)求该抛物线的解析式和对称轴,并写出线段BC的中点坐标;
(2)将线段BC先向左平移2个单位长度,在向下平移m个单位长度,使点C的对应点C1恰好落在该抛物线上,求此时点C1的坐标和m的值;
(3)若点P是该抛物线上的动点,点Q是该抛物线对称轴上的动点,当以P,Q,B,C四点为顶点的四边形是平行四边形时,求此时点P的坐标.
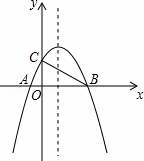
解:(1)∵抛物线y=ax2+bx﹣3a(a≠0)与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,2),
∴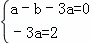 ,
,
解得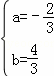 .
.
∴抛物线的解析式为y=﹣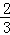 x2+
x2+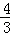 x+2=﹣
x+2=﹣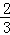 (x﹣1)2+2
(x﹣1)2+2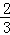 ,
,
∴对称轴是x=1,
∵1+(1+1)=3,
∴B点坐标为(3,0),
∴BC的中点坐标为(1.5,1);
(2)∵线段BC先向左平移2个单位长度,再向下平移m个单位长度,使点C的对应点C1恰好落在该抛物线上,
∴点C1的横坐标为﹣2,
当x=﹣2时,y=﹣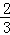 ×(﹣2)2+
×(﹣2)2+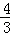 ×(﹣2)+2=﹣
×(﹣2)+2=﹣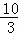 ,
,
∴点C1的坐标为(﹣2,﹣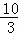 ),
),
m=2﹣(﹣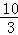 )=5
)=5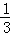 ;
;
(3)①若BC为平行四边形的一边,
∵BC的横坐标的差为3,
∵点Q的横坐标为1,
∴P的横坐标为4或﹣2,
∵P在抛物线上,
∴P的纵坐标为﹣3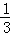 ,
,
∴P1(4,﹣3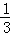 ),P2(﹣2,﹣3
),P2(﹣2,﹣3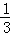 );
);
②若BC为平行四边形的对角线,
则BC与PQ互相平分,
∵点Q的横坐标为1,BC的中点坐标为(1.5,1),
∴P点的横坐标为1.5+(1.5﹣1)=2,
∴P的纵坐标为﹣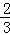 ×22+
×22+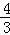 ×2+2=2,
×2+2=2,
∴P3(2,2).
综上所述,点P的坐标为:P1(4,﹣3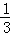 ),P2(﹣2,﹣3
),P2(﹣2,﹣3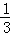 ),P3(2,2).
),P3(2,2).


科目:初中数学 来源: 题型:
若a=(-3)13 -(-3)14,b=(-0.6)12 -(-0.6)14,c=(-1.5)11 -(-1.5)13,则下列有关a、b、c的大
小关系,何者正确? (A) a > b > c (B) a > c > b (C) b > c > a (D) c > b > a
查看答案和解析>>
科目:初中数学 来源: 题型:
如图(十三),矩形ABCD的外接圆O与水平地面相切于A点,圆O半径为2,且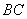 =2
=2 。若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了75p,则此时哪一弧与地面相切?
。若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了75p,则此时哪一弧与地面相切?
(A)  (B)
(B)  (C)
(C)  (D)
(D) 
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,直线AB与x轴交于点A,与y轴交于点C(0,2),且与反比例函数y=﹣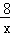 的图象在第二象限内交于点B,过点B作BD⊥x轴于点D,OD=2.
的图象在第二象限内交于点B,过点B作BD⊥x轴于点D,OD=2.
(1)求直线AB的解析式;
(2)若点P是线段BD上一点,且△PBC的面积等于3,求点P的坐标.
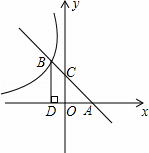
查看答案和解析>>
科目:初中数学 来源: 题型:
2014年6月4日据经济日报报道:青海格尔木枸杞已进入国际市场,远销美国、欧盟、东南亚等国家和地区,出口创汇达4000000美元,将4000000美元用科学记数法表示为 美元.
查看答案和解析>>
科目:初中数学 来源: 题型:
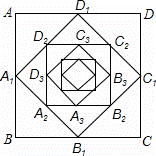
如图,顺次连接边长为1的正方形ABCD四边的中点,得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1的中点,得到四边形A2B2C2D2,再顺次连接四边形A2B2C2D2四边的中点,得到四边形A3B3C3D3,…,按此方法得到的四边形A8B8C8D8的周长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com