
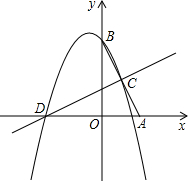
解:(1)过C作CD⊥x轴于G,
∵点C为线段AB的中点,
∴CG是△OAB的中位线,
∴点C的坐标是(1,2),
又∵OA=2,OB=4,
∴AB=

,AC=

,
显然△ABO∽△ADC,
∴

,
即

,
∴AD=5OD=AD-OA=3,
∴点D的坐标是(-3,0);
(2)解:设过B(0,4),C(1,2),D(-3,0)的抛物线的关系式为y=ax
2+bx+c,
∴

,
解得:

,
∴抛物线的关系式为

;
(3)解:设点P的坐标为(x,y)连BD,过点P作PH⊥x轴于H,交BD于E

,
S
四边形PBCD=S
△BCD+S
△PBD,
∵S
△BCD=S
△ACD为定值,
∴要使四边形PBCD的面积最大就是使△PBD的面积最大,
①当P在BD间的抛物线上时,即-3<x<0,
S
△PBD=S
△PBE+S
△PED=

PE×DH+

PE×OH=

PE×OD=

PE,
∵PE=PH-EH=y
P-y
E,
直线BD的关系式为y=
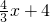
,

∴PE=

,
=

,
当x=

时,PE最大为
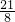
,
∴点P的坐标(

,

),
②当P在BC间的抛物线上时,即0<x<1,
同理可求出四边形PBCD的面积,
很显然,此时四边形PBCD的面积要小于点P在BD间的抛物线上时的四边形PBCD的面积,
故P点的坐标是(

,

).
分析:(1)首先过C作CD⊥x轴于G.构造△OAB的中位线CG,根据A、B点的坐标及三角形中位线的性质不难求得点C的坐标.由于△ABO∽△ADC,利用相似三角形的性质解得AD的长,那么D点的坐标也就确定.
(2)运用待定系数法求解.假设过B(0,4),C(1,2),D(-3,0)的抛物线的关系式为y=ax
2+bx+c,将三点坐标值代入联立组成三元一次方程组解得a、b、c的值.
(3)设点P的坐标为(x,y)连BD,过点P作PH⊥x轴于H,交BD于E.观察图象发现S
四边形PBCD=S
△BCD+S
△PBD,
因为S
△BCD=S
△ACD为定值,所以要使四边形PBCD的面积最大就是使△PBD的面积最大.再分别就①当P在BD间的抛物线上时(即-3<x<0);②当P在BC间的抛物线上时(即0<x<1)时,讨论x的取值,进而得到P点的坐标,并验证结果的合理性.
点评:本题是二次函数的综合题型,其中涉及到的知识点有利用待定系数法求抛物线的解析式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果;并有效利用了坐标与线段的数形结合.

 轴于D,
轴于D, 解:(1)过C作CD⊥x轴于G,
解:(1)过C作CD⊥x轴于G, ,AC=
,AC= ,
, ,
, ,
, ,
, ,
, ;
; ,
, PE×DH+
PE×DH+ PE×OH=
PE×OH= PE×OD=
PE×OD= PE,
PE,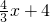 ,
,
 ,
, ,
, 时,PE最大为
时,PE最大为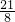 ,
, ,
, ),
), ,
, ).
).


 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: