
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD; ②求证:CF=CH; ③判断△CFH的形状并说明理由.

证明:(1)∵△ABC和△CDE都是等边三角形,
∴BC=AC,CE=CD,∠BCA=∠ECD=60°,
∴∠BCA+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,
∴在△BCE和△ACD中,
∵ BC=AC ∠BCE=∠ACD CE=CD
∴△BCE≌△ACD (SAS).
(2) ∵ △ABC和△CDE都是等边三角形 ∴ AC=BC,CD=CE,∠BCE=∠ACD=120º
∴ △ECB≌△DCA
∴ ∠FEC=∠ADC,CD=CE
∵ ∠HCD=∠FCE=60º
∴ △ECF≌△DCH
∴ CF=CH
(3)由(1)知△BCE≌△ACD,∴∠CBF=∠CAH,BC=AC
又∵△ABC和△CDE都是等边三角形,且点B、C、D在同一条直线上
∴∠ACH=180°-∠ACB-∠HCD=60°=∠BCF
∴在△BCF和△ACH中, 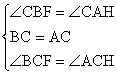
∴△BCF≌△ACH (ASA)
∴CF=CH又∵∠FCH=60°∴△CHF为等边三角形
∴∠FHC=∠HCD=60°∴FH‖BD


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,先把梯形ABCD向左平移6个单位长度得到梯形A1B1C1D1
(1)请你在平面直角坐标系中画出梯形A1B1C1D1;(2)以x轴为对称轴,画出(1)中的对称梯形A2B2C2D2,并写出它们的顶点坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知函数y = 3x + b和y = ax - 3的图象交于点P( -2,-5) ,则根据图象可得不等式3x + b >ax - 3的解集是 .
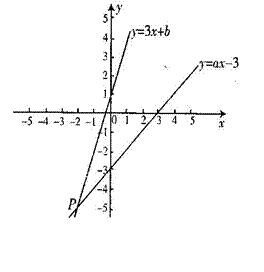
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com