
 ���������κ���ͼ��Ķ��㡢���ڷ�����ͬ��������������κ���Ϊ��ͬ�ض��κ�������
���������κ���ͼ��Ķ��㡢���ڷ�����ͬ��������������κ���Ϊ��ͬ�ض��κ����������� ��1�����ݡ�ͬ�ض��κ������Ķ��壬ֻҪ���������Ķ��㡢���ڷ���һ�����ɣ�
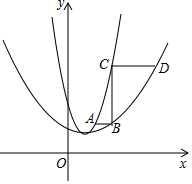
��2���ٰ�P���������y1=2x2-4mx+2m2+1�������m��ֵ�������������ʽ����y1�Ľ���ʽ������䶥�����꣬��ɵ�y2�Ķ������꣬��������y2�Ľ���ʽ�������B������Ϊ��n��$\frac{1}{4}$��n-1��2+1����n��1������AB��CD��x���BC��AB���ö��κ���ͼ���ϵ�������������ɵó���B��C��D�����꣬�ٸ��������ľ�������AB��CD�ij��ȣ��������$\frac{CD}{AB}$���ɵó����ۣ�
��� �⣺��1����y=x2��y=2x2�Ķ����Ϊ��0��0�����ҿ������ϣ�
��y=x2��y=2x2Ϊ��ͬ�ض��κ�������
��2���ٰ�P��1��1������y1=2x2-4mx+2m2+1��
�ã�1=2-4m+2m2+1����ã�m=1��
��y1=2x2-4x+3=2��x-1��2+1��
��y2��y1Ϊ��ͬ�ض��κ�������
�ඥ��һ��Ϊ��1��1������y2=a��x-1��2+1��
��a+1=$\frac{5}{4}$��
��a=$\frac{1}{4}$��
�ຯ��y2�ı���ʽΪy2=$\frac{1}{4}$��x-1��2+1=$\frac{1}{4}$x2-$\frac{1}{2}$x+$\frac{5}{4}$��
�����B��������n��$\frac{1}{4}$��n-1��2+1����n��1����
��AB��x�ᣬ
���A��������$\frac{\sqrt{2}}{4}$��n-1��+1��$\frac{1}{4}$��n-1��2+1����
��AB��CD��x�ᣬBC��AB��
���C��������n��2��n-1��2+1������D��������2$\sqrt{2}$��n-1��+1��2��n-1��2+1����
��AB=n-[$\frac{\sqrt{2}}{4}$��n-1��+1]=��n-1����1-$\frac{\sqrt{2}}{4}$����CD=2$\sqrt{2}$��n-1��+1-n=��n-1����2$\sqrt{2}$-1����
��$\frac{CD}{AB}$=$\frac{��n-1����2\sqrt{2}-1��}{��n-1����1-\frac{\sqrt{2}}{4}��}$=$\frac{2\sqrt{2}-1}{\frac{4-\sqrt{2}}{4}}$=2$\sqrt{2}$��
���� ���⿼���ˡ�ͬ�ض��κ������Ķ��塢����ϵ��������κ�������ʽ�����κ���ͼ���ϵ������������ƽ���ߵ������Լ������ľ��룬����Ĺؼ��ǣ���1�����ݡ�ͬ�ض��κ������Ķ���д�����κ�������2�������ô���ϵ���������������ʽ�������ö��κ���ͼ���ϵ�����������ҳ���B��C��D�����꣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڵȱߡ�ABC�У�ADƽ�֡�BAC��BC���D����EΪAC�ߵ��е㣬BC=8����AD����һ����Q����QC+QE����СֵΪ4$\sqrt{3}$��
��ͼ���ڵȱߡ�ABC�У�ADƽ�֡�BAC��BC���D����EΪAC�ߵ��е㣬BC=8����AD����һ����Q����QC+QE����СֵΪ4$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=-��x-1��2+4 | B�� | y=��x-1��2+2 | C�� | y=��x+1��2+2 | D�� | y=��x-2��2+3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
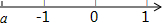 ������a�������϶�Ӧ�ĵ���ͼ��ʾ����a��-a��1�Ĵ�С��ϵ��ȷ���ǣ�������
������a�������϶�Ӧ�ĵ���ͼ��ʾ����a��-a��1�Ĵ�С��ϵ��ȷ���ǣ�������| A�� | -a��a��1 | B�� | a��-a��1 | C�� | 1��-a��a | D�� | a��1��-a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
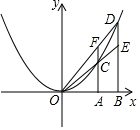 ��ͼ����x����������A��m��0����B��n��0����n��m��0�����ֱ����A����B��x��Ĵ��ߣ���������y=x2�ڵ�C����D��ֱ��OC��ֱ��BD�ڵ�E��ֱ��OD��ֱ��AC�ڵ�F����E����F��������ֱ����yE��yF
��ͼ����x����������A��m��0����B��n��0����n��m��0�����ֱ����A����B��x��Ĵ��ߣ���������y=x2�ڵ�C����D��ֱ��OC��ֱ��BD�ڵ�E��ֱ��OD��ֱ��AC�ڵ�F����E����F��������ֱ����yE��yF�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com