练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    解方程：（3x-1）2-25=0．
    考点：平方根
    专题：
    分析：把（3x-1）看作一个整体，利用平方根的定义列出方程求解即可．
    解答：解：移项得，（3x-1）2=25，
    因此，3x-1=5或3x-1=-5，
    解得x=2或x=-
    4
    3
    ．
    点评：本题考查了平方根的定义，是基础题熟记概念是解题的关键，注意整体思想的利用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    解方程
    （1）
    2y-1
    3
    =
    y+2
    4
    -1
    （2）
    3y-1
    4
    -1=
    5y-7
    6
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算
    （1）12-（-18）+（-7）-15                 
    （2）（-8）+4÷（-2）
    （2）（-10）÷（-
    1
    5
    ）×5             
    （4）（-
    1
    2
    +
    2
    3
    -
    1
    4
    ）×|-24|

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，AB∥CD，AD∥BC，∠B=50°，∠EDA=60°，求∠CDO．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    开口向下的抛物线y=（m2-2）x2+3mx+1的对称轴经过点（-1，3），则m=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    大客车上原有（3a+b）人，中途下车一半人，又上车若干人，此时车上共乘客（8a-b）人，问上车乘客是多少人？当a=10，b=8时，上车的乘客是多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知线段AB，延长AB到点C，使BC=
    2
    3
    AB，反向延长AB到点D，使AD=
    3
    2
    AB，E是线段DC的中点，若AE=2cm．求线段AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，在Rt△ACB中，∠BAC=90°，AB=AC，分别过B、C两点作过点A的直线l的垂线，垂足为D、E；

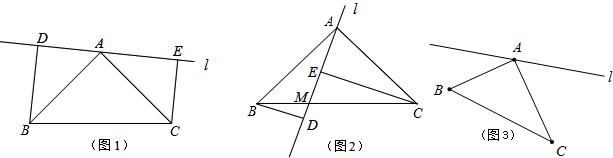
    （1）如图1，当D、E两点在直线BC的同侧时，猜想，BD、CE、DE三条线段有怎样的数量关系？并说明理由．
    （2）如图2，当D、E两点在直线BC的两侧时，BD、CE、DE三条线段的数量关系为
     
    ．
    （3）如图2，若直线AD被截成的线段AE、EM、MD的长度分别是a，b，c，又S△ABM=S1，S△ACM=S2，求S2-S1的值（用含有a，b，c的代数式表示）
    （4）如图，∠BAC=90°，AB=22，AC=28．点P从B点出发沿B-A-C路径向终点C运动；点Q从C点出发沿C-A-B路径向终点B运动．点P和Q分别以每秒2和3个单位的速度同时开始运动，只要有一点到达相应的终点时两点同时停止运动；在运动过程中，分别过P和Q作PF⊥l于F，QG⊥l于G．问：点P运动多少秒时，△PFA与△QAG全等？（直接写出结果即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在Rt△ABC中，∠C=90°．根据下列条件求出直角三角形的其他元素．
    （1）c=40，∠A=60°；
    （2）a=4
    		6
    ，b=12
    		2
    ．

    查看答案和解析>>

    同步练习册答案