
已知:抛物线y=x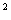 +bx+c的顶点D在直线y=-4x上,且与x轴的交点A(-1,0),B,交y轴于点C,顶点为D.
+bx+c的顶点D在直线y=-4x上,且与x轴的交点A(-1,0),B,交y轴于点C,顶点为D.

(1) 求抛物线的解析式及顶点D的坐标.
(2)试判断点C与以BD为直径的⊙M的位置关系.
(3)若点P的坐标是(a,0),是否存在a,使得直线PC是⊙M的切线?若存在,求出a的值,若不存在,请说明理由.
(1) y=x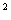 -2x-3,顶点D(1,-4) (2) 点C在⊙M上(3) 存在,-3/2
-2x-3,顶点D(1,-4) (2) 点C在⊙M上(3) 存在,-3/2
【解析】⑴y=x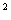 -2x-3,顶点D(1,-4),
-2x-3,顶点D(1,-4),
⑵∵抛物线y=x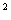 -2x-3与x轴的校点为B(3,0)
-2x-3与x轴的校点为B(3,0)
∴BD中点M为(2,-2),
∵BD=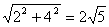 ,CM=
,CM=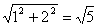 ,
,
∴BD=2CM ,
∴点C在⊙M上。
⑶存在。
过点M作MN⊥y轴于N点,
则MN=2,NC=1.
当PC与⊙M相切时,
∠MCP=∠COB=90°,
又∠AQC=∠CQP,
∴△QAC∽△QCP
∴∠CPO=∠MCO,
∴tan∠MCO=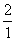 ,tan∠CPO=
,tan∠CPO=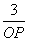 ,
,
∴OP=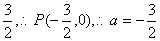
(1)首先求出抛物线的项点表达式,并把它代入直线方程中,然后把A点坐标代抛物线方程中,联立解出b、c的值,从而得出抛物线的解析式,再求出抛物线与直线的交点D的坐标;
(2)先求出BD和CM的值,然后根据BD=2CM ,得出点C在⊙M上;
(3)存在.过点M作MN⊥y轴于N点,由PC与⊙M相切,得出△QAC∽△QCP,得出∠CPO=∠MCO,从而求OP的长度,得出a的值。


科目:初中数学 来源: 题型:
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com