
在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式.
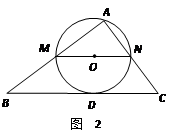
解:(1)∵MN∥BC,∴∠AMN=∠B,∠ANM=∠C.
∴△AMN ∽△ABC.
∴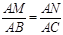 ,即
,即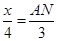 .
.
∴AN=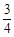 x.
x.
∴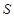 =
= .(0<
.(0<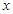 <4)
<4)
(2)如图2,设直线BC与⊙O相切于点D,连结AO,OD,则AO="OD" =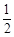 MN.
MN.
在Rt△ABC中,BC =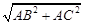 =5.
=5.
由(1)知 △AMN ∽△ABC.
∴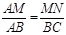 ,即
,即 .
.
∴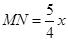 ,
,
∴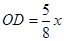 .
.
过M点作MQ⊥BC于Q,则 .
.
在Rt△BMQ与Rt△BCA中,∠B是公共角,
∴△BMQ∽△BCA.
∴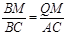 .
.
∴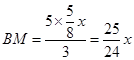 ,
,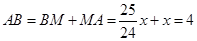 .
.
∴x= .
.
∴ 当x= 时,⊙O与直线BC相切.
时,⊙O与直线BC相切.
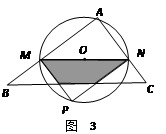
(3)随点M的运动,当P点落在直线BC上时,连结AP,则O点为AP的中点.
∵MN∥BC,∴∠AMN=∠B,∠AOM=∠APC.
∴△AMO ∽△ABP.
∴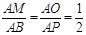 . AM=MB=2.
. AM=MB=2.
故以下分两种情况讨论:
① 当0<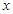 ≤2时,
≤2时, .
.
② 当2<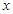 <4时,设PM,PN分别交BC于E,F.
<4时,设PM,PN分别交BC于E,F.
∵ 四边形AMPN是矩形,
∴PN∥AM,PN=AM=x.
又∵ MN∥BC,
∴ 四边形MBFN是平行四边形.
∴ FN=BM=4-x.
∴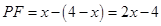 .
.
又△PEF ∽△ACB.
∴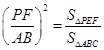 .
.
∴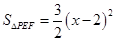 .
.  =
=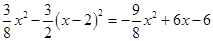 .
.
解析


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2012年初中毕业升学考试(广西桂林卷)数学(带解析) 题型:解答题
如图,在△ABC中,∠BAC=90°,AB=AC=6,D为BC的中点.
(1)若E、F分别是AB、AC上的点,且AE=CF,求证:△AED≌△CFD;
(2)当点F、E分别从C、A两点同时出发,以每秒1个单位长度的速度沿CA、AB运动,到点A、B
时停止;设△DEF的面积为y,F点运动的时间为x,求y与x的函数关系式;
(3)在(2)的条件下,点F、E分别沿CA、AB的延长线继续运动,求此时y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2013届辽宁省大石桥市水源二中九年级上学期阶段检测数学试卷(带解析) 题型:解答题
在△ABC中,AB=AC,∠BAC=α,点D是BC上一动点(不与B、C重合),将线段AD绕点A逆时针旋转α后到达AE位置,连接DE、CE,设∠BCE=β.
(1)如图1,若α=90°,求β的大小;
(2)如图2,当点D在线段BC上运动时,试探究α与β之间的数量关系,并证明你的结论;
(3)当点D在线段BC的反向延长线上运动时(画出图形),(2)中的结论是否仍然成立?若成立,请证明,若不成立,请直接写出α与β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源:人教版初三年级数学相似形提高测试 题型:填空题
如图,在△ABC中,AB=AC=27,D在AC上,且BD=BC=18,DE∥BC交AB于E,则DE=_______.
查看答案和解析>>
科目:初中数学 来源:2013届江苏省镇江市初一四月月考数学卷 题型:解答题
如图,在ΔABC中,AB=AC=10,BC=8.用尺规作图作BC边上的中线AD(保留作图痕迹,不要求写作法、证明),并求AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com