
在△ABC中,∠A=90°,AB=8,AC=6,M是AB上的动点(不与A、B重合),过M作MN//BC交AC于点N,以MN为直径作⊙O,设AM=x
(1)用含x的代数式表示△AMN的面积S;
(2)M在AB上运动,当⊙O与BC相切时(如图①),求x的值;
(3)M在AB上运动,当⊙O与BC相交时(如图②),在⊙O上取一点P,使PM//AC,连接PN,PM交BC于E,PN交BC于点F,设梯形MNFE的面积为y,求y关于x的函数关系式。
解:(1)∵MN//BC,∴∠AMN=∠B,∠ANM=∠C
∴△AMN∽△ABC……………………………………………………………(1分)
∴![]() ,即
,即![]() ,∴
,∴![]()
∵AM⊥AN,∴![]() …………………(3分)
…………………(3分)
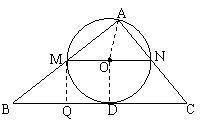 (2)设BC与⊙O相切于点D,连接AO、OD,
(2)设BC与⊙O相切于点D,连接AO、OD,
则AO=OD=![]() MN
MN
在Rt△ABC中,![]()
又∵△AMN∽△ABC,
∴![]() ,即
,即![]() ,∴
,∴![]() ,∴
,∴![]() ………………………(4分)
………………………(4分)
过M作MQ⊥BC于Q,则![]()
则△BMQ∽△ABC,
∴![]() ,∴
,∴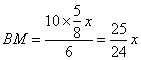
∵![]()
∴![]() …………………………………………………………………………(6分)
…………………………………………………………………………(6分)
(3)∵∠A=90°,PM//AC,∠MPN=90°
∴四边形AMPN是矩形…………………(7分)
∴PN=AM=x
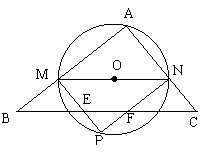 又∵四边形BFNM是平行四边形,
又∵四边形BFNM是平行四边形,
∴FN=BM=8-x,PF=PN-FN=x-(8-x)=2x-8…(8分)
又Rt△PEF∽Rt△ABC,∴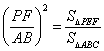 ,
,
∴![]()
∵![]()
∴![]() ………(10分)
………(10分)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com