
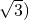 ,将线段OA绕坐标原点O逆时针旋转90°,得
,将线段OA绕坐标原点O逆时针旋转90°,得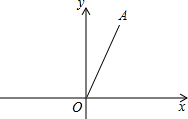 到线段OB.
到线段OB.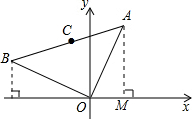 解:(1)作AM⊥ox轴于M,作BN⊥ox轴于N,
解:(1)作AM⊥ox轴于M,作BN⊥ox轴于N,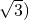 ,所以BN=1,
,所以BN=1,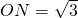 ,
, ,1),
,1),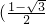 ,
,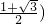 ,
,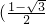 ,
,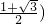 代入得
代入得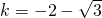 ,
, .
.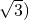 ,将线段OA绕坐标原点O逆时针旋转90°,得到线段OB,要求B点的坐标,所以可作AM⊥ox轴于M,作BN⊥ox轴于N,因为∠AOB=90°,所以∠OAM=∠BON,且OA=OB,所以Rt△AMO≌Rt△ONB,结合A点的坐标可求出BN=1,
,将线段OA绕坐标原点O逆时针旋转90°,得到线段OB,要求B点的坐标,所以可作AM⊥ox轴于M,作BN⊥ox轴于N,因为∠AOB=90°,所以∠OAM=∠BON,且OA=OB,所以Rt△AMO≌Rt△ONB,结合A点的坐标可求出BN=1,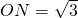 ,又因点B在第二象限,所以点B的坐标为
,又因点B在第二象限,所以点B的坐标为 ,1);
,1); ,进而求出解析式.
,进而求出解析式.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源: 题型:
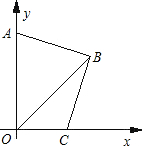 如图,在直角坐标系中,B点的坐标为(a,b),且a、b满足
如图,在直角坐标系中,B点的坐标为(a,b),且a、b满足| a+b-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:

| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com