
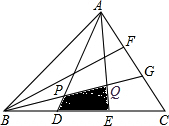
 如图,△ABC的面积为1,D,E,F,G分别是BC,AC上的三等分点,求阴影四边形PQED的面积.
如图,△ABC的面积为1,D,E,F,G分别是BC,AC上的三等分点,求阴影四边形PQED的面积. 分析 连结PC,先求出△BPC的面积,再得出△BPD面积,进而可求四边形PQED的面积.
解答 解:连结PC,如图: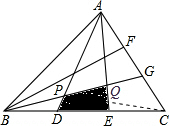
设S△BPD=a,S△CPG=b,
则S△PDC=2a,S△PGA=2b,
则$\left\{\begin{array}{l}{3a+b=\frac{1}{3}}\\{2a+3b=\frac{2}{3}}\end{array}\right.$,
解得a=$\frac{1}{21}$,b=$\frac{4}{21}$.
故S四边形PQED=S△BGC-S△BPD-S四边形EQGC=$\frac{1}{3}$-$\frac{1}{21}$-$\frac{1}{6}$=$\frac{5}{42}$.
点评 本题考查三角形的面积结合二元一次方程组的应用,求一些关系复杂的图形面积,代数化是一个重要技巧,利用代数化,能清晰明朗地表示图形面积之间的关系,从而可以化解或降低问题的难度.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:选择题
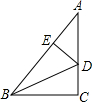 如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为( )
如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为( )| A. | $\frac{2}{3}$cm | B. | $\frac{3}{2}$cm | C. | 2cm | D. | $\frac{3}{2}\sqrt{5}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
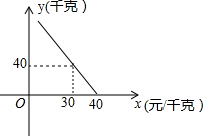 某超市对进货价位20元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
某超市对进货价位20元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
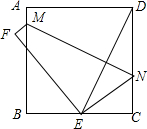 将一张边长为4cm的正方形纸片沿MN对折,使点D落在BC边上.
将一张边长为4cm的正方形纸片沿MN对折,使点D落在BC边上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com