
如图16,已知△ABC为等边三角形,P为BC上一点,△APQ为等边三角形。
(1)求证:AB∥CQ;
(2)AQ与CQ能否互相垂直?若能互相垂直,指出点P在BC上的位置,并给予证明;若AQ与CQ不能互相垂直,请说明理由。
 |
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
| 1 |
| 6 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 16 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•峨眉山市二模)选做题:从甲、乙两题中选做一题,如果两题都做,只以甲题计分.
(2013•峨眉山市二模)选做题:从甲、乙两题中选做一题,如果两题都做,只以甲题计分.| 1 |
| 2 |
| k |
| x |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
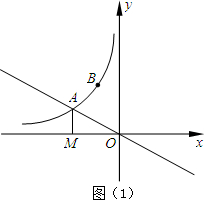 选做题:从甲、乙两题中选做一题,如果两题都做,只以甲题计分.
选做题:从甲、乙两题中选做一题,如果两题都做,只以甲题计分. 的图象与反比例函数
的图象与反比例函数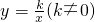 在第二象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.
在第二象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.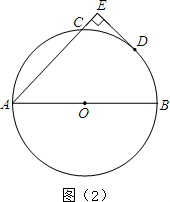
查看答案和解析>>
科目:初中数学 来源: 题型:
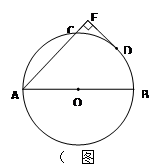
如图7,已知AB、AC分别为⊙O的直径和弦,D为⌒BC的中点,DE⊥AC于E,DE=6,AC=16.
1.求证:DE是⊙O的切线.
2.求直径AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com