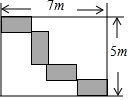
如图是某居民小区内的矩形工地.工地里有四块相同的小矩形绿化区域．小矩形的边都与工地的边平行.每个矩形由顶点连接.求小矩形的长和宽．题目和参考答案——青夏教育精英家教网—

9．

如图是某居民小区内的矩形工地，工地里有四块相同的小矩形绿化区域．小矩形的边都与工地的边平行，每个矩形由顶点连接，求小矩形的长和宽．

分析根据题意和图形可以列出相应的方程组，从而可以解答本题．

解答解：设小矩形的长为xm，宽为ym，
$\left\{\begin{array}{l}{3x+y=7}\\{x+3y=5}\end{array}\right.$，得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$，
答：小矩形的长为2m，宽为1m．

点评本题考查二元一次方程组的应用，解答本题的关键是明确题意，列出相应的方程组，利用数形结合的思想解答．

练习册系列答案

实验班全程提优训练系列答案

天利38套对接高考单元专题测试卷系列答案

全程测评试卷系列答案

每时每课期中期末课时单元系列答案

全优考典单元检测卷及归类总复习系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

11．

为了解今年全县2000名初二学生“创新能力大赛”的笔试情况，随机抽取了部分同学的成绩，整理并制作如图所示的图表（部分未完成）．请你根据提供的信息，解答下列问题：
（1）此次调查的样本容量为400．
（2）在表中：m=160；n=0.3；h=0.4．
（3）补全频数分布直方图；
（4）根据频数分布表、频数分布直方图，你获得哪些信息？

分数段	频数	频率
60≤x＜70	40	0.1
70≤x≤80	120	n
80≤x＜90	m	h
90≤x＜100	80	0.2

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

12．如图①，在△ABC中，∠BAC=90°，AB=AC，点E在AC上（且不与点A，C重合），在△ABC的外部作△CED，使∠CED=90°，DE=CE，连接AD，分别以AB，AD为邻边作平行四边形ABFD，连接AF．
（1）请直接写出线段AF，AE的数量关系AF=$\sqrt{2}$AE；
（2）将△CED绕点C逆时针旋转，当点E在线段BC上时，如图②，连接AE，请判断线段AF，AE的数量关系，并证明你的结论．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

17．如图1，已知⊙O的半径为1，∠PAQ的正切值为$\frac{{\sqrt{3}}}{6}$，AQ是⊙O的切线，将⊙O从点A开始沿射线AQ的方向滚动，切点为A'．
（1）sin∠PAQ=$\frac{\sqrt{13}}{13}$，cos∠PAQ=$\frac{2\sqrt{39}}{13}$；
（2）①如图1，当⊙O在初始位置时，圆心O到射线AP的距离为$\frac{2\sqrt{39}}{13}$；
②如图2，当⊙O的圆心在射线AP上时，AA'=2$\sqrt{3}$．
（3）在⊙O的滚动过程中，设A与A'之间的距离为m，圆心O到射线AP的距离为n，求n与m之间的函数关系式，并探究当m分别在何范围时，⊙O与射线AP相交、相切、相离．