
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 等腰三角形要判断腰长的情况,本题可先设P点的坐标,根据OA是底边、腰几种情况下手进行讨论即可得出答案.
解答 解:已知△AOP的边OA,这条边可能是底边也可能是腰
当OA是底边时,点P是OA的垂直平分线与x轴,y轴的交点,这两个点的坐标是(2,0)和(0,-2)满足条件的有两点;
当OA是腰时,当O是顶角顶点时,以O为圆心,以OA为半径作圆,与两坐标轴的交点坐标是(0,2$\sqrt{2}$),(0,-2$\sqrt{2}$),(2$\sqrt{2}$,0),(-2$\sqrt{2}$,0);
当A是顶角顶点时,以A为圆心,以AO为半径作圆,与两坐标轴的交点坐标有除原点以外有两个交点,因而使△AOP为等腰三角形,则符合条件的点P有8个.
故选D
点评 本题考查了等腰三角形的判定;分情况进行讨论,能够把各种情况能够讨论全是解决本题的关键.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:解答题
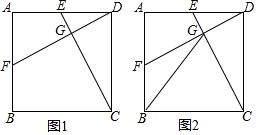 如图1,已知:正方形ABCD,点E为AD上一点,连接CE,过点D作DG⊥CE于G交AB于F.
如图1,已知:正方形ABCD,点E为AD上一点,连接CE,过点D作DG⊥CE于G交AB于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com