
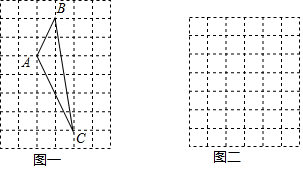
分析 (1)先构造直角三角形,然后依据勾股定理求得AB、AC、BC的长,从而可求得△ABC的周长,依据△ABC的面积=矩形DCEF的面积-3个直角三角形的面积求解即可;
(2)依据勾股定理确定出DE、DF、EF的长,然后依据(1)中方法将三角形的面积转化为一个矩形的面积与3个直角三角形的面积之差求解即可.
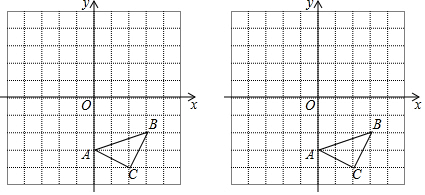
解答 解:(1)如图所示: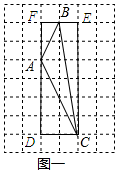
依据勾股定理可知AB=$\sqrt{F{B}^{2}+A{F}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
BC=$\sqrt{B{E}^{2}+E{C}^{2}}$=$\sqrt{{1}^{2}+{6}^{2}}$=$\sqrt{37}$,
AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$.
∴AB+BC+AC=$\sqrt{5}$+$\sqrt{37}$+2$\sqrt{5}$=3$\sqrt{5}$+$\sqrt{37}$.
△ABC的面积=矩形DCEF的面积-△ADC的面积-△AFB的面积-△BEC的面积=6×2-$\frac{1}{2}$×4×2-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×6=4.
(2)如图所示: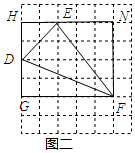
△DEF的面积=矩形GFNH的面积-△DGF的面积-△ENF的面积-△DHE的面积=4×5-$\frac{1}{2}$×5×2-$\frac{1}{2}$×4×3-$\frac{1}{2}$×2×2=7.
点评 本题主要考查的是勾股定理的应用,将△ABC和△DEF的面积转化为一个矩形的面积与3个直角三角形的面积之差求解即可.


科目:初中数学 来源: 题型:填空题
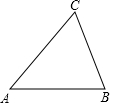 如图有一张面积为10的三角形ABC纸片,其中AB为5,把它剪两刀拼成一个矩形(无缝隙、无重叠),且矩形的一边与AB平行,则矩形的周长为14或10.
如图有一张面积为10的三角形ABC纸片,其中AB为5,把它剪两刀拼成一个矩形(无缝隙、无重叠),且矩形的一边与AB平行,则矩形的周长为14或10.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
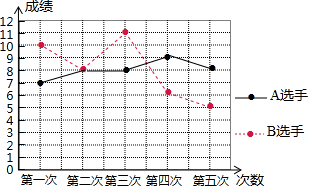 2022年将在北京-张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示:则下列说法中正确的是( )
2022年将在北京-张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示:则下列说法中正确的是( )| A. | SA2>SB2,应该选取B选手参加比赛 | B. | SA2<SB2,应该选取A选手参加比赛 | ||
| C. | SA2≥SB2,应该选取B选手参加比赛 | D. | SA2≤SB2,应该选取A选手参加比赛 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图①所示是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
如图①所示是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
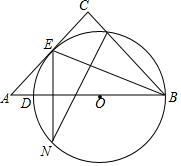 如图,在△ABC中,∠C=90°,D为AB边上一点,以DB为直径的⊙O与AC相切于点E,与BC相交于点F,FN⊥BE交⊙O于点N.
如图,在△ABC中,∠C=90°,D为AB边上一点,以DB为直径的⊙O与AC相切于点E,与BC相交于点F,FN⊥BE交⊙O于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com