
 如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡脚为45°的上坡向上走到C处,这时,PC=20$\sqrt{2}$m,点C与点A在同一水平线上,A、B、P、C在同一平面内.
如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡脚为45°的上坡向上走到C处,这时,PC=20$\sqrt{2}$m,点C与点A在同一水平线上,A、B、P、C在同一平面内.分析 (1)首先分析图形:根据题意构造直角三角形,利用在Rt△CPE中,由sin45°=$\frac{CE}{PC}$,得出EC的长度,进而可求出答案;
(2)在Rt△CPE中,tan60°=$\frac{AB}{BP}$,得出BP的长,进而得出PE的长,即可得出答案.
解答 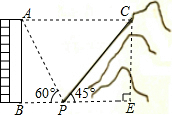 解:(1)过点C作CE⊥BP于点E,
解:(1)过点C作CE⊥BP于点E,
在Rt△CPE中,∵PC=20$\sqrt{2}$m,∠CPE=45°,
∴sin45°=$\frac{CE}{PC}$,
∴CE=PC•sin45°=20$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=20m,
∵点C与点A在同一水平线上,
∴AB=CE=20m,
答:居民楼AB的高度约为20m;
(2)在Rt△ABP中,∵∠APB=60°,
∴tan60°=$\frac{AB}{BP}$,
∴BP=$\frac{20}{\sqrt{3}}$=$\frac{20\sqrt{3}}{3}$m,
∵PE=CE=20m,
∴AC=BE=($\frac{20\sqrt{3}}{3}$+20)m,
答:C、A之间的距离为($\frac{20\sqrt{3}}{3}$+20)m.
点评 此题主要考查了解直角三角形的应用-仰角俯角问题,要求学生借助仰角、坡角关系构造直角三角形,并结合图形利用三角函数求解.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
 如图,已知A、B、C、D是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.
如图,已知A、B、C、D是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间t(天) | 1 | 3 | 5 | 10 | 36 | … |
| 日销售量m(件) | 94 | 90 | 86 | 76 | 24 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图所示.
已知:如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
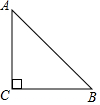 如图,△ABC中,∠C=90°,CA=CB=1,将△ABC绕点B顺时针旋转45°,得到△DBE(A、D两点为对应点),画出旋转后的图形,并求出线段AE的长.
如图,△ABC中,∠C=90°,CA=CB=1,将△ABC绕点B顺时针旋转45°,得到△DBE(A、D两点为对应点),画出旋转后的图形,并求出线段AE的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com