
 如图,矩形ABCD中,AB=2BC,E是AB上一点,O是CD上一点,以OC为半径作⊙O,将△ADE折叠至△A′DE,点A′在⊙O上,延长EA′交BC延长线于F,且恰好过点O,过点D作⊙O的切线交BC延长线于点G.若FG=1,则AD=2,⊙O半径=$\frac{3}{2}$.
如图,矩形ABCD中,AB=2BC,E是AB上一点,O是CD上一点,以OC为半径作⊙O,将△ADE折叠至△A′DE,点A′在⊙O上,延长EA′交BC延长线于F,且恰好过点O,过点D作⊙O的切线交BC延长线于点G.若FG=1,则AD=2,⊙O半径=$\frac{3}{2}$. 分析 作OH⊥DG于H,如图,设DA=x,则AB=2x,根据折叠的性质得DA′=DA=x,∠DA′E=∠A=90°,则可判断DA′与⊙O相切,再证明△DOA′≌△FOC得到DA′=CF=x,接着根据切线的性质得H点为切点,于是利用切线长定理得DH=DA′=x,GH=GC=CF+GF=x+1,然后在Rt△DCG中根据勾股定理得(2x)2+(x+1)2=(x+x+1)2,解得x1=0(舍去),x2=2,即AD=2;设⊙O的半径为r,则OC=OA′=r,OD=2x-r=4-r,根据勾股定理得到22+r2=(4-r)2,解得r=$\frac{3}{2}$,即⊙O的半径为$\frac{3}{2}$.
解答 解:作OH⊥DG于H,如图,设DA=x,则AB=2x,
∵△ADE折叠至△A′DE,
∴DA′=DA=x,∠DA′E=∠A=90°,
∴DA′与⊙O相切,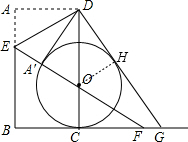
在△ODA′和△OCF中
$\left\{\begin{array}{l}{∠DA′O=∠FCO}\\{OA′=OC}\\{∠DOA′=∠FOC}\end{array}\right.$
∴△DOA′≌△FOC.
∴DA′=CF=x,
∵DG是⊙O的切线,OH⊥DG,
∴H点为切点,
∴DH=DA′=x,GH=GC=CF+GF=x+1,
在Rt△DCG中,∵DC2+CG2=DG2,
∴(2x)2+(x+1)2=(x+x+1)2,解得x1=0(舍去),x2=2,
∴AD=2,
设⊙O的半径为r,则OC=OA′=r,OD=2x-r=4-r,
在Rt△DOA′中,∵DA′2+OA′2=DO2,
∴22+r2=(4-r)2,解得r=$\frac{3}{2}$,
即⊙O的半径为$\frac{3}{2}$.
故答案为2,$\frac{3}{2}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了折叠的性质和勾股定理.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| 密码 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 对应数字 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
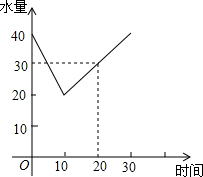 一蓄水池中有水40m3,水池里的水量与放水时间有如下关系:
一蓄水池中有水40m3,水池里的水量与放水时间有如下关系:| 放水时间/分 | 2 | 4 | 6 | 8 | … |
| 水池中水量/m3 | 36 | 32 | 28 | 24 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 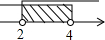 | B. | 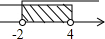 | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com