
 的一元二次方程
的一元二次方程 有实数根,则
有实数根,则 的取值范围是___________
的取值范围是___________ 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
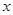 个队,该小组共赛了90场,那么列出正确的方程是 。
个队,该小组共赛了90场,那么列出正确的方程是 。 查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,所以
,所以 ,即:
,即: 有最小值1,此时
有最小值1,此时 ;同样,因为
;同样,因为 ,所以
,所以 ,即
,即 有最大值6,此时
有最大值6,此时 。
。 = 时,代数式
= 时,代数式 有最 (填写大或小)值为 。②当
有最 (填写大或小)值为 。②当 = 时,代数式
= 时,代数式 有最 (填写大或小)值为 。
有最 (填写大或小)值为 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com