C
分析:利用全等的判定可判断出①,利用反推法判断②,过点P作PM⊥AB于M,也是利用反推法得出矛盾,从而判断出③,过点P作PM⊥AB于M,过点E作EN⊥AB于点N,利用中位线的知识可求出HP,过点P作PM⊥AB于点M,作PL⊥BC于点L,则根据中位线的知识,可得出PM=2,PL=1,先求出S
△AFC,继而可得出S
△ABC的值.
解答:(1)由于AD=BC,CE=DE,∠BCE=∠ADE,所以△DAE≌△CBE,BE=AE,所以①正确;
(2)由于△EBC不是等边三角形而是等腰三角形,而P是BE中点,所以AP并不垂直于BR,BE=2EP,只有当∠BPE=90°时sin∠EBP=

,但∠EPA并不等于90°,所以②不正确;
(3)过点P作PM⊥AB于M,
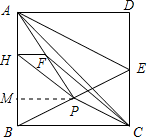
由于F是AP中点,则HF是△APM的一条中位线,即H是AM中点,不是AB中点,故HP不是△BAE的中位线,也就可得出HP不平行AE,所以③错误;
(4)过点P作PM⊥AB于M,过点E作EN⊥AB于点N,
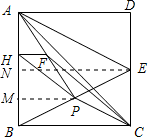
由点P是BE中点可得PM是△PNE的中位线,PM=

NE=2,(3)得出了HF是△APM的中位线,HF=

PM,故可得HF=

PM=1,故④正确;
(5)
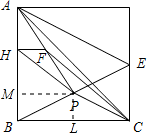
过点P作PM⊥AB于点M,作PL⊥BC于点L,则根据中位线的知识,可得出PM=2,PL=1,从而求出S
△APC=S
△ABC-S
△ABP-S
△BPC=8-2-4=2,
再由AF=FP可得S
△AFC=

S
△ABC=1,故⑤正确.
综上可得①④⑤正确,共三个.
故选C.
点评:此题考查了正方形的性质、三角形的中位线定理,全等三角形的判定与性质,关键是熟练各个知识点的内容,熟记一些基本定理,达到解题过程中,各个知识点融会贯通.

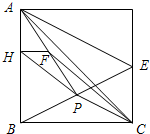 如图,已知边长为4的正方形ABCD中,E为CD中点,P为BE中点,F为AP中点,FH⊥AB交AB于H,连接PH.则下列结论正确的有
如图,已知边长为4的正方形ABCD中,E为CD中点,P为BE中点,F为AP中点,FH⊥AB交AB于H,连接PH.则下列结论正确的有 ;③HP∥AE;④HF=1;⑤S△AFC=1.
;③HP∥AE;④HF=1;⑤S△AFC=1. ,但∠EPA并不等于90°,所以②不正确;
,但∠EPA并不等于90°,所以②不正确;

 NE=2,(3)得出了HF是△APM的中位线,HF=
NE=2,(3)得出了HF是△APM的中位线,HF= PM,故可得HF=
PM,故可得HF= PM=1,故④正确;
PM=1,故④正确;
 S△ABC=1,故⑤正确.
S△ABC=1,故⑤正确.

 如图,已知边长为4的正方形ABCD中,E为AD中点,P为CE中点,F为BP中点,FH⊥BC交BC于H,连接PH,则下列结论正确的是( )
如图,已知边长为4的正方形ABCD中,E为AD中点,P为CE中点,F为BP中点,FH⊥BC交BC于H,连接PH,则下列结论正确的是( )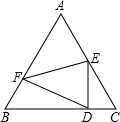 如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则CE的长是( )
如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则CE的长是( )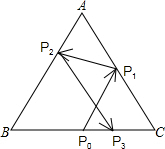 如图,已知边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角),且1<BP3<
如图,已知边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角),且1<BP3< 用三角函数中正切的两角和公式:tan(α+β)=(tanα+tanβ)÷(1-tanα•tanβ),求出∠CAC′+∠CAA′的度数.( )
用三角函数中正切的两角和公式:tan(α+β)=(tanα+tanβ)÷(1-tanα•tanβ),求出∠CAC′+∠CAA′的度数.( )