先阅读短文,再解答短文后面的问题.
在几何学中,通常用点表示位置,用线段的长度表示两点间的距离,用一条射线表示一个方向.在平面内,从一点出发的所有射线,可以用来表示平面内的各个不同的方向.
在线段的两个端点中,我们规定一个顺序:A为始点,B为终点,我们就说线段AB具有射线AB的方向.具有方向的线段,叫做有向线段.通常在有向线段的终点处画上箭头表示它的方向.以A为始点,以B为终点的有向线段记作
.应注意,始点一定要写在终点的前面.
已知有向线段
,线段AB的长度叫做有向线
的长度(或模),
的长度记作|
|.有向线段包含三个要素:始点、方向和长度.知道了有向线段的始点,它的终点就被方向和长度所唯一确定.
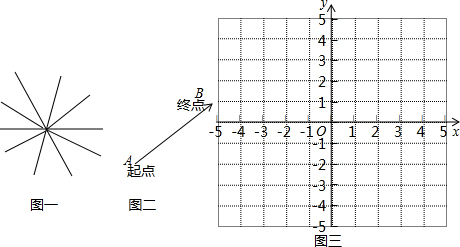
解答下列问题:
(1)如果两条有向线段的长度相同,始点的位置相同,那么它们的终点位置是否相同?为什么?
(2)如果两条有向线段的方向相同,始点的位置相同,那么它们的终点位置是否相同?为什么?
(3)在平面直角坐标系中画出下列有向线段(有向线段与轴的长度单位相同):
①|
|=
2,
确与x轴的负半轴的夹角是45°,且与y轴的正半轴的夹角是45°,求终点A的坐标;
②
的终点B的坐标为(3,
),求它的模及它与x轴的正半轴的夹角;
(4)已知点M、A、P在同一直线上;那么
||+||=||一定成立吗?请在图中画出图形并加以说明.



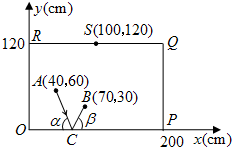 实验探究:下面设想用电脑模拟台球游戏,为简单起见,约定:①每个球或球袋都视为一点,如不遇障碍,各球均沿直线前进;②A球击中B球,意味着B球在A球前进的路线上,且B球被撞击后沿着A球原来的方向前进;③球撞及桌边后的反弹角等于入射角.
实验探究:下面设想用电脑模拟台球游戏,为简单起见,约定:①每个球或球袋都视为一点,如不遇障碍,各球均沿直线前进;②A球击中B球,意味着B球在A球前进的路线上,且B球被撞击后沿着A球原来的方向前进;③球撞及桌边后的反弹角等于入射角.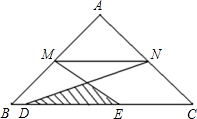 如图所示,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连接DN、EM,若AB=10cm,BC=16cm,DE=8cm,则图中阴影部分的面积为( )
如图所示,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连接DN、EM,若AB=10cm,BC=16cm,DE=8cm,则图中阴影部分的面积为( )
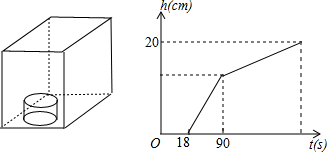 .水槽中水面上升的高度h与注水时间t之间的函数关系如图所示.
.水槽中水面上升的高度h与注水时间t之间的函数关系如图所示.