
 ,且抛物线与x轴交于整数点(坐标为整数的点),求此抛物线的解析式.
,且抛物线与x轴交于整数点(坐标为整数的点),求此抛物线的解析式. ,根据公式法求出ax2-4ax+4a-2=0的根,再由题意抛物线与x轴交于整数点(坐标为整数的点),来确定a的值,从而求出抛物线的解析式.
,根据公式法求出ax2-4ax+4a-2=0的根,再由题意抛物线与x轴交于整数点(坐标为整数的点),来确定a的值,从而求出抛物线的解析式. =
= 是整数,
是整数, 是整数;(3分)
是整数;(3分) 是整数的完全平方数.∵
是整数的完全平方数.∵ ,
, ,(4分)
,(4分) 取1,4,
取1,4, 时,a=2;当
时,a=2;当 时,
时, .
. ,
, .(6分)
.(6分)

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源:2010年北京市昌平区中考数学一模试卷(解析版) 题型:解答题
 ,1)关于x轴的对称点为C,AC与x轴交于点B,将△OCB沿OC翻折后,点B落在点D处.
,1)关于x轴的对称点为C,AC与x轴交于点B,将△OCB沿OC翻折后,点B落在点D处.
查看答案和解析>>
科目:初中数学 来源:2010年北京市昌平区中考数学一模试卷(解析版) 题型:解答题
 的图象都经过点A(3,3),将直线y=kx向下平移后得直线l,设直线l与反比例函数的图象的一个分支交于点B(6,n).
的图象都经过点A(3,3),将直线y=kx向下平移后得直线l,设直线l与反比例函数的图象的一个分支交于点B(6,n).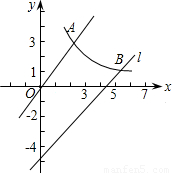
查看答案和解析>>
科目:初中数学 来源:2011年山东省济宁市曲阜市实验中学九年级数学第一次摸底试卷(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2010年北京市昌平区中考数学一模试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com