
分析 (1)由AC=7,BC=5,得到AB=2,由M是AB的中点,得到BM=1,于是得到结论;
(2)①C在线段AB上,求得CM=$\frac{1}{2}$(b-a),②点C在线段BA的延长线上,求得CM=AC+AM=a+$\frac{1}{2}$(b-a)=$\frac{1}{2}$(a+b).
解答 解:(1)∵AC=7,BC=5,
∴AB=2,
∵M是AB的中点,
∴BM=1,
∴CM=6,
故答案为:6;
(2)①C在线段AB上,
∵AC=a,BC=b,
∴AB=AC+BC=a+b,
∵点M是AB的中点,
∴BM=$\frac{1}{2}$AB=$\frac{1}{2}$(a+b),
∴CM=$\frac{1}{2}$(b-a),
②点C在线段BA的延长线上,
∵AC=a,BC=b,且a<b,
∴AB=b-a,
∵点M是AB的中点,
∴AM=$\frac{1}{2}$(b-a),
∴CM=AC+AM=a+$\frac{1}{2}$(b-a)=$\frac{1}{2}$(a+b),
故答案为:$\frac{1}{2}$(b-a)或$\frac{1}{2}$(a+b).
点评 本题考查了两点间的距离,利用了线段的和差,线段中点的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
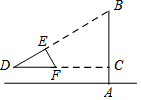 如图,小南用自制的直角三角形纸板DEF测量树的高度AB,他使斜边DF保持水平,并且边DE与点B在同一直线上.己知三角形的两条直角边DE=0.6m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.
如图,小南用自制的直角三角形纸板DEF测量树的高度AB,他使斜边DF保持水平,并且边DE与点B在同一直线上.己知三角形的两条直角边DE=0.6m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 据新华网消息,2016年6月20日,使用中国自主芯片制造的超级计算机“神威太湖之光”以浮点运算速度每秒930000000亿次登上全球500强榜首,数字930000000用科学记数法可表示为( )
据新华网消息,2016年6月20日,使用中国自主芯片制造的超级计算机“神威太湖之光”以浮点运算速度每秒930000000亿次登上全球500强榜首,数字930000000用科学记数法可表示为( )| A. | 9.3×108 | B. | 93×107 | C. | 0.93×109 | D. | 9.3×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
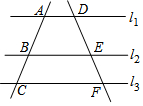 如图,直线l1∥l2∥l3,直线AC依次交l1、l2、l3于A、B、C三点,直线DF依次交l1、l2、l3于D、E、F三点,若$\frac{AB}{AC}$=$\frac{4}{7}$,DE=2,求EF的长.
如图,直线l1∥l2∥l3,直线AC依次交l1、l2、l3于A、B、C三点,直线DF依次交l1、l2、l3于D、E、F三点,若$\frac{AB}{AC}$=$\frac{4}{7}$,DE=2,求EF的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
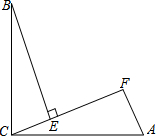 如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0°<∠ACF<45°.
如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0°<∠ACF<45°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A(a,b)在第一象限,AB⊥x轴于点B.C为边0A的中点.在边OB从小于AB到大于AB的变化过程中.若a+b的值始终保持不变,则在经过动点C的反比例函数y=$\frac{k}{x}$(k≠0)中k的值的变化情况是( )
如图,点A(a,b)在第一象限,AB⊥x轴于点B.C为边0A的中点.在边OB从小于AB到大于AB的变化过程中.若a+b的值始终保持不变,则在经过动点C的反比例函数y=$\frac{k}{x}$(k≠0)中k的值的变化情况是( )| A. | 一直增大 | B. | 一直不变 | C. | 先增大后减小 | D. | 先减小后增大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com