
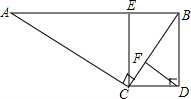
 如图,AB∥CD,∠ACB=∠BDC=Rt∠,CE⊥AB于点E,DF⊥CB于点F.
如图,AB∥CD,∠ACB=∠BDC=Rt∠,CE⊥AB于点E,DF⊥CB于点F. 的值.
的值.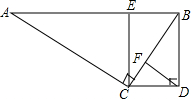 (1)证明:∵AB∥CD,
(1)证明:∵AB∥CD,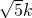 .
. =
= =
= =
= =
= .
.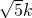 ,再由△ABC∽△BCD,根据相似三角形对应角相等得出∠BAC=∠CBD,则sin∠BAC=sin∠CBD,然后根据CE=BD及正弦函数的定义列出比例式,即可求出
,再由△ABC∽△BCD,根据相似三角形对应角相等得出∠BAC=∠CBD,则sin∠BAC=sin∠CBD,然后根据CE=BD及正弦函数的定义列出比例式,即可求出 的值.
的值.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com