
 如图,E、F分别是矩形ABCD的BC边和CD边上的点,且S△ABE=3,S△ECF=8,S△ADF=5,则矩形ABCD的面积为________.
如图,E、F分别是矩形ABCD的BC边和CD边上的点,且S△ABE=3,S△ECF=8,S△ADF=5,则矩形ABCD的面积为________. 解:如图,
解:如图, AB•BE=3,
AB•BE=3, EC•CF=8,
EC•CF=8, AD•DF=5,
AD•DF=5, EC•CF=8可知,EC•CF=16,
EC•CF=8可知,EC•CF=16, =
= =
= (在两个矩形中,长和宽如有一边对应相等,那么对应的另一边的比等于两个矩形面积的比),
(在两个矩形中,长和宽如有一边对应相等,那么对应的另一边的比等于两个矩形面积的比), ,
, ,
, +x=3×2=6,
+x=3×2=6,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系xoy中,矩型ABCD的边AB在x轴上,且AB=3,BC=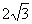 ,直线y=
,直线y=![]() 经过点C,交y轴于点G
经过点C,交y轴于点G

1.点C、D的坐标分别是C( ),D( )
2.求顶点在直线y=![]() 上且经过点C、D的抛物线的解析式
上且经过点C、D的抛物线的解析式
3.将(2)中的抛物线沿直线y=![]() 平移,平移后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
平移,平移后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
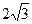 ,直线y=
,直线y=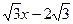 经过点C,交y轴于点G
经过点C,交y轴于点G
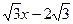 上且经过点C、D的抛物线的解析式
上且经过点C、D的抛物线的解析式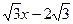 平移,平移后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
平移,平移后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。查看答案和解析>>
科目:初中数学 来源:2011年安徽省中考压轴题预测试数学卷 题型:解答题
如图,在平面直角坐标系xoy中,矩型ABCD的边AB在x轴上,且AB=3,BC=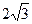 ,直线y=
,直线y=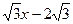 经过点C,交y轴于点G
经过点C,交y轴于点G
【小题1】点C、D的坐标分别是C( ),D( )
【小题2】求顶点在直线y=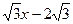 上且经过点C、D的抛物线的解析式
上且经过点C、D的抛物线的解析式
【小题3】将(2)中的抛物线沿直线y=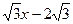 平移,平移后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
平移,平移后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2011年安徽省中考压轴题预测试数学卷 题型:选择题
如图,在平面直角坐标系xoy中,矩型ABCD的边AB在x轴上,且AB=3,BC=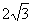 ,直线y=
,直线y=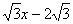 经过点C,交y轴于点G
经过点C,交y轴于点G
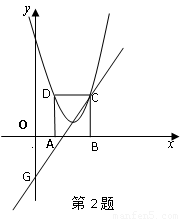
1.点C、D的坐标分别是C( ),D( )
2.求顶点在直线y=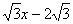 上且经过点C、D的抛物线的解析式
上且经过点C、D的抛物线的解析式
3.将(2)中的抛物线沿直线y=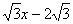 平移,平移后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
平移,平移后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com