Question

10．已知在平面直角坐标系xOy中（如图），抛物线y=ax²-4与x轴的负半轴相交于点A，与y轴相交于点B，AB=2$\sqrt{5}$，点P在抛物线上，线段AP与y轴的正半轴交于点C，线段BP与x轴相交于点D，设点P的横坐标为m．
（1）求这条抛物线的解析式；
（2）用含m的代数式表示线段CO的长；
（3）当tan∠ODC=$\frac{3}{2}$时，求∠PAD的正弦值．

Answer 1

分析 （1）根据已知条件先求出OB的长，再根据勾股定理得出OA=2，求出点A的坐标，再把点A的坐标代入y=ax²-4，求出a的值，从而求出解析式；
（2）根据点P的横坐标得出点P的坐标，过点P作PE⊥x轴于点E，得出OE=m，PE=m²-4，从而求出AE=2+m，再根据$\frac{OC}{PE}$=$\frac{AO}{AE}$，求出OC；
（3）根据tan∠ODC=$\frac{3}{2}$，得出$\frac{OC}{OD}$=$\frac{3}{2}$，求出OD和OC，再根据△ODB∽△EDP，得出$\frac{OD}{ED}$=$\frac{OB}{EP}$，求出OC，求出∠PAD=45°，从而求出∠PAD的正弦值．

解答 解：（1）∵抛物线y=ax²-4与y轴相交于点B，
∴点B的坐标是（0，-4），
∴OB=4，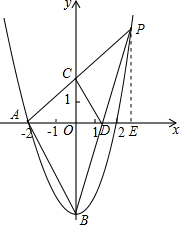
∵AB=2$\sqrt{5}$，
∴OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=2，
∴点A的坐标为（-2，0），
把（-2，0）代入y=ax²-4得：0=4a-4，
解得：a=1，
则抛物线的解析式是：y=x²-4；

（2）方法一：
∵点P的横坐标为m，
∴点P的坐标为（m，m²-4），
过点P作PE⊥x轴于点E，
∴OE=m，PE=m²-4，
∴AE=2+m，
∵$\frac{OC}{PE}$=$\frac{AO}{AE}$，
∴$\frac{OC}{{m}^{2}-4}$=$\frac{2}{2+m}$，
∴CO=2m-4；
方法二：
∵点P在抛物线上，∴P（m，m²-4），
设PA的直线方程为：y=kx+b，
∴$\left.\begin{array}{l}{km+b={m}^{2}-4}\\{-2k+b=0}\end{array}\right\}$⇒$\left\{\begin{array}{l}{k=m-2}\\{b=2m-4}\end{array}\right.$，
∴l_PA：y=（m-2）x+2m-4，
∴CO=2m-4；

（3）方法一：
∵tan∠ODC=$\frac{3}{2}$，
∴$\frac{OC}{OD}$=$\frac{3}{2}$，
∴OD=$\frac{2}{3}$OC=$\frac{2}{3}$×（2m-4）=$\frac{4m-8}{3}$，
∵△ODB∽△EDP，
∴$\frac{OD}{ED}$=$\frac{OB}{EP}$，
∴$\frac{\frac{4m-8}{3}}{\frac{8-m}{3}}$=$\frac{4}{{m}^{2}-4}$，
∴m₁=-1（舍去），m₂=3，
∴OC=2×3-4=2，
∵OA=2，
∴OA=OC，
∴∠PAD=45°，
∴sin∠PAD=sin45°=$\frac{\sqrt{2}}{2}$．

方法二：
∵P（m，m²-4），B（0，-4），
∴l_PB：y=mx-4，
∴D（$\frac{4}{m}$，0），
tan∠ODC=$\frac{3}{2}$⇒$\frac{OC}{OD}=\frac{3}{2}$，OC=2m-4，
∴OD=$\frac{4m-8}{3}$，
∵线段AP与y轴的正半轴交于点C，
∴OC=2m-4（m＞2），
∴$\frac{4m-8}{3}=\frac{4}{m}$，
经整理：m²-2m-3=0，
∴m₁=-1（舍去），m₂=3，
∴P（3，5），
∴l_PA：y=x+2，
∴∠PAD=45°，
∴sin∠PAD=$\frac{\sqrt{2}}{2}$．

点评 此题考查了二次函数的综合，用到的知识点是相似三角形的判定与性质、勾股定理、特殊角的三角函数值，关键是根据题意作出辅助线，构造相似三角形．