练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．如果$\sqrt{x+2}$=4，则$\root{3}{x+13}$=（　　）
    A．16B．3C．±3D．14

    分析 首先根据平方根的含义和求法，求出x的值是多少；然后根据立方根的含义和求法求解即可．

    解答 解：∵$\sqrt{x+2}$=4，
    ∴x+2=42=16，
    解得x=14，
    ∴$\root{3}{x+13}$
    =$\root{3}{14+13}$
    =$\root{3}{27}$
    =3
    故选：B．

    点评 此题主要考查了平方根、立方根的概念的运用，要熟练掌握，解答此题的关键是求出x的值是多少．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．（1）利用计算器计算：$\sqrt{9×9+19}$=10；
    （2）利用计算器计算：$\sqrt{99×99+199}$=100；
    （3）利用计算器计算：$\sqrt{999×999+1999}$=1000；
    （4）利用计算器计算：$\sqrt{\underset{\underbrace{99…9}}{n}×\underset{\underbrace{99…9}}{n}+1\underset{\underbrace{99…+9}}{n}}$=1000000…（后面n个0）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．把二次函数y=x2+bx+c的图象向下平移2个单位，再向左平移3个单位．得到二次函数y=x2+3x-1的图象．求b和c的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，已知线段m，n，p，求作△ABC，使AB=m，AC=n，AD=p，D为BC边上的中点，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算：
    （1）$\sqrt{12}$-$\sqrt{\frac{1}{3}}$；
    （2）$\sqrt{20}$×$\sqrt{5}$-8；
    （3）$\frac{\sqrt{8}}{2}$+2$\sqrt{18}$-$\frac{1}{4}$$\sqrt{32}$；
    （4）-6$\sqrt{7}$×$\frac{1}{3}$$\sqrt{21}$÷2$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．算式（-66+$\frac{3}{17}$）×$\frac{1}{3}$可化为（　　）
    A．-66×$\frac{1}{3}$+$\frac{3}{17}$×$\frac{1}{3}$B．-66×$\frac{1}{3}$-$\frac{3}{17}$×$\frac{1}{3}$C．-66×3+$\frac{3}{17}$×3D．-66×3-$\frac{3}{17}$×3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．计算：
    （1）（-2）+（+5）-（-3）+（-7）；
    （2）（-2）-（+3）-（-7）-（-5）+（-1）-（+6）；
    （3）（+$\frac{1}{3}$）+（-$\frac{1}{2}$）-（-$\frac{5}{6}$）；
    （4）0-（-6）-（+7）-（-8）+（+9）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

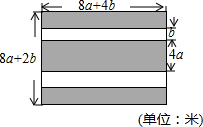    16．2015年9月7日河北青年报报道，针对机动车数量快速增长带来的停车难等问题，住房和城乡建设都引导各城市加快编制城市停车设施专项规划，逐步缓解城市停车矛盾．某大型商超前有块长方形空地，该商场计划将此块空地修建成停车场，其设计图如图所示（阴影部分为停车位，两个小阴影部分的面积相等，空白部分为甬道，两条甬道的宽相等）
    （1）用含a，b的式子表示停车位的总面积；
    （2）已知a=2.5，b=4，若每个停车位的宽为2.4米，长为5.5米，求该商场计划修建的停车场的车位数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．（1）如图1，在正方形ABCD中，M是BC边（不含端点B，C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点，若∠AMN=90°，求证：AM=MN．
    （2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图2），N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．

    查看答案和解析>>

    同步练习册答案