
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
|
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 6 |


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
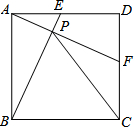 如图,正方形ABCD中,点E从点A出发沿着AD向D运动,(点E不与点A,点D重合)同时点F从点D出发沿着线段DC向C运动,(点F不与点D,点C重合)点E与F点运动速度相同,当点E停止运动时,另一动点F随之停止运动,设BE与AF相交于点P,连接PC请研究:
如图,正方形ABCD中,点E从点A出发沿着AD向D运动,(点E不与点A,点D重合)同时点F从点D出发沿着线段DC向C运动,(点F不与点D,点C重合)点E与F点运动速度相同,当点E停止运动时,另一动点F随之停止运动,设BE与AF相交于点P,连接PC请研究:查看答案和解析>>
科目:初中数学 来源: 题型:
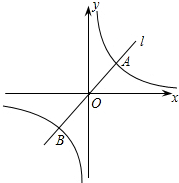 我们知道,y=x的图象向右平移1个单位得到y=x-1的图象,类似的,y=
我们知道,y=x的图象向右平移1个单位得到y=x-1的图象,类似的,y=| k |
| x |
| k |
| x+2 |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 任意抛掷一枚均匀的骰子(各个面上的点数为1-6),将第一次,第二次抛掷的点数分别记为m,n
任意抛掷一枚均匀的骰子(各个面上的点数为1-6),将第一次,第二次抛掷的点数分别记为m,n查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com