
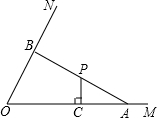
 长线上一点,连接AP并延长与射线ON交于点B.
长线上一点,连接AP并延长与射线ON交于点B.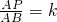 ,是否存在适当的k,使得
,是否存在适当的k,使得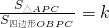 ?若存在,试求出k的值;若不存在,试说明理由.
?若存在,试求出k的值;若不存在,试说明理由.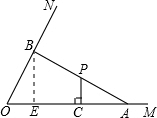 解:(1)△AOB为直角三角形.理由如下:
解:(1)△AOB为直角三角形.理由如下: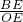 =2,
=2, a
a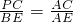 ,
, =
=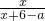 ,
,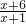 ,
,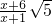 ,
,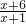 •
•
 -1;
-1;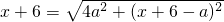
 ;
;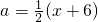 ,解得x=1;
,解得x=1;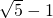 、
、 、1时,△AOB是等腰三角形.
、1时,△AOB是等腰三角形. •x•2=x,S△ABO=
•x•2=x,S△ABO= •2a•(x+6)=(x+6)a,
•2a•(x+6)=(x+6)a,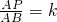 ,得
,得 =
=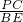 =
= ,
,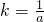 ,
,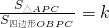 ,
,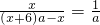 ,
,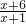 ,
,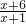 =x,
=x,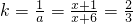 .
. a,设CA=x,由PC∥BE,则
a,设CA=x,由PC∥BE,则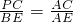 ,可得到a=
,可得到a=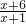 ,然后分类讨论:若OA=OB,即x+6=
,然后分类讨论:若OA=OB,即x+6=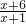 •
• ;若AO=AB,即
;若AO=AB,即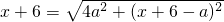 ;若OB=AB时,OE=EA,
;若OB=AB时,OE=EA,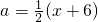 ,分别解方程即可得到x的值;
,分别解方程即可得到x的值; •x•2=x,S△ABO=
•x•2=x,S△ABO= •2a•(x+6)=(x+6)a,由
•2a•(x+6)=(x+6)a,由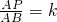 ,得
,得 =
=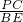 =
= ,得到
,得到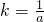 ,再根据题意得到
,再根据题意得到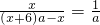 ,而a=
,而a=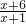 ,即可得到关于x的方程,解方程即可.
,即可得到关于x的方程,解方程即可.

 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
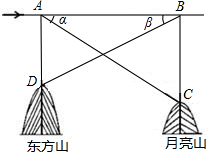 5987,tanβ=0.15847,若飞机的飞行速度为180米/秒,则该飞机从A到B处需多少时间?(精确到0.1秒)
5987,tanβ=0.15847,若飞机的飞行速度为180米/秒,则该飞机从A到B处需多少时间?(精确到0.1秒)查看答案和解析>>
科目:初中数学 来源: 题型:
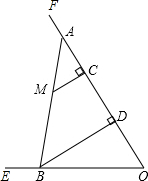 (2013•杭州一模)如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.
(2013•杭州一模)如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 5987,tanβ=0.15847,若飞机的飞行速度为180米/秒,则该飞机从A到B处需多少时间?(精确到0.1秒)
5987,tanβ=0.15847,若飞机的飞行速度为180米/秒,则该飞机从A到B处需多少时间?(精确到0.1秒)查看答案和解析>>
科目:初中数学 来源:2011年湖北省黄石市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com