Question

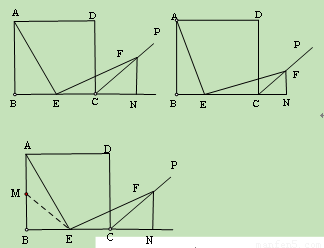
（2011内蒙古赤峰，25，14分）如图（图1、图2），四边形ABCD是边长为4的正方形，点E在线段BC上，∠AEF=90°，且EF交正方形外角平分线CP于点F，FN⊥BC，交BC的延长线于点N。

（1）若点E是BC的中点（如图1），AE与EF相等吗？为什么？

（2）点E在BC间运动时（如图2），设BE=x, △ECF的面积为y。

①求y与x的函数关系式；

②当x取何值时，y有最大值，并求出这个最大值。

 

Answer 1

【答案】

解：（1）相等。

理由：∵四边形ABCD是正方形，点E是BC的中点

∴∠B=∠DCN=90°. AB=BC=2BE，

∴∠BAE+∠BEA=90°.

∵∠AEF=90°

∴∠AEB+∠FEC=90°.，

∴∠BAE=∠FEN.

∵CF是∠DCN的角平分线，∠FNC=90°。

∴∠FCN=∠CFN=45°.

∴FN=CN.

在Rt△ABE和Rt△ENF中

∴EN=2FN，∴EC＋CN=2CN，∴FN=BE .

∴Rt△ABE≌Rt△ENF.

∴AE=EF.

方法二：如图，取AB的中点M，连结ME. 

∵四边形ABCD是正方形，

∴AB=BC，∠B=∠DCN=90°，

∵点E是BC的中点

∴AM=MB=BE=EC

在Rt△MBE中，∠BME=∠BEM=45°.

∴∠AME=135°；

∵CF是∠DCN的角平分线，

∴∠FCN=45°.

∴∠ECF=135°.

∴∠AME=∠ECF ；

∵∠AEF=90°  ；

∴∠AEB+∠FEC=90° ；

在Rt△ABE中，∠BAE+∠AEB=90°.

∴∠BAE=∠FEN  ；

∴△AME≌△ECF ；

∴AE=EF 。

∴BE(EC+CN)=CN(BE+EC) ;

∴BE·EC＋ BE·CN = BE·CN ＋CN·EC ;

∴BE·EC = CN·EC ;

∴BE = CN  ;

∴BE =FN = x ，     

∴。

②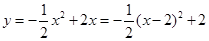

当x =2时，y有最大值为2.

【解析】略