
 的解,点C是直线
的解,点C是直线 与直线AB的交点,点D在线段OC上,OD=
与直线AB的交点,点D在线段OC上,OD=
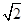 ,3
,3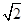 ) Q2(3
) Q2(3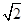 ,-3
,-3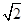 ) Q3(3,-3) Q4(6,6)
) Q3(3,-3) Q4(6,6)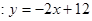 ……………………………………1分
……………………………………1分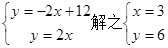 ……………………………………2分
……………………………………2分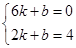 ……………………………………1分
……………………………………1分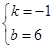
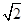 ,3
,3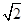 )……………………………………………………………1分
)……………………………………………………………1分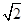 ,-3
,-3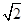 )………………………………………………………………1分
)………………………………………………………………1分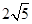 ,由勾股定理可求出a的值,从而求得点D的坐标,把A、D的坐标代入,利用方程组即可求解;
,由勾股定理可求出a的值,从而求得点D的坐标,把A、D的坐标代入,利用方程组即可求解;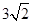 ,OM=6-
,OM=6-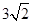 ,即P(6-
,即P(6-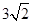 ,
,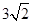 ),所以Q的横坐标为6-
),所以Q的横坐标为6-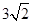 -6=-
-6=-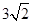 ,Q1(-
,Q1(-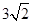 ,
,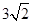 );若P在x轴下方,OAPQ是菱形,则PQ∥OA,PQ=OA=6=AP.过P作PM⊥x轴,因为∠MAP=∠OAD=45°,利用三角函数可求出PM=AM=
);若P在x轴下方,OAPQ是菱形,则PQ∥OA,PQ=OA=6=AP.过P作PM⊥x轴,因为∠MAP=∠OAD=45°,利用三角函数可求出PM=AM=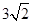 ,OM=6+
,OM=6+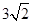 ,即P(6+
,即P(6+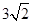 ,-
,-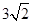 ),所以Q的横坐标为6+
),所以Q的横坐标为6+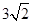 -6=
-6=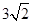 ,Q2(
,Q2(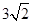 ,-
,-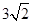 );若Q在x轴上方,OAQP是菱形,则∠OAQ=2∠OAD=90°,所以此时OAQP是正方形.又因正方形边长为6,所以此时Q(6,6);若Q在x轴下方,OPAQ是菱形,则∠PAQ=2∠OAD=90°,所以此时OPAQ是正方形.又因正方形对角线为6,由正方形的对称性可得Q(3,-3).
);若Q在x轴上方,OAQP是菱形,则∠OAQ=2∠OAD=90°,所以此时OAQP是正方形.又因正方形边长为6,所以此时Q(6,6);若Q在x轴下方,OPAQ是菱形,则∠PAQ=2∠OAD=90°,所以此时OPAQ是正方形.又因正方形对角线为6,由正方形的对称性可得Q(3,-3).

 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源:不详 题型:解答题
 与
与 轴、
轴、 轴分别相交于点
轴分别相交于点 、
、 .抛物线
.抛物线 与
与 轴的正半轴相交于点
轴的正半轴相交于点 ,与这个一次函数的图像相交于
,与这个一次函数的图像相交于 、
、 ,且
,且 .
.
 、
、 、
、 的坐标;
的坐标; ,求抛物线
,求抛物线 的解析式.
的解析式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
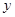 (单位:百万平方米),与时间
(单位:百万平方米),与时间 的关系是
的关系是 ,(
,( 单位:年,
单位:年, 且
且 为整数);后4年,每年竣工投入使用的公租房面积
为整数);后4年,每年竣工投入使用的公租房面积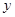 (单位:百万平方米),与时间
(单位:百万平方米),与时间 的关系是
的关系是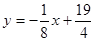 (
( 单位:年,
单位:年,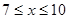 且
且 为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第
为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第 年投入使用的公租房的租金z(单位:元/m2)与时间
年投入使用的公租房的租金z(单位:元/m2)与时间 (单位:年,
(单位:年,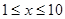 且
且 为整数)满足一次函数关系如下表:
为整数)满足一次函数关系如下表:| z(元/m2) | 50 | 52 | 54 | 56 | 58 | ... |
 (年) (年) | 1 | 2 | 3 | 4 | 5 | ... |
 的函数关系式;
的函数关系式;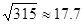 ,
, ,
,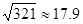 )
)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 型产品40件,
型产品40件, 型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:| |  型利润 型利润 |  型利润 型利润 |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
 型产品
型产品 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为 (元),求
(元),求 关于
关于 的函数关系式,并求出
的函数关系式,并求出 的取值范围;
的取值范围;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com