
在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38 ①,然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39 ②,
②一①得:3S―S=39-1,即2S=39-1,
∴S= .
.
得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是___________.
科目:初中数学 来源:2016年初中毕业升学考试(湖北宜昌卷)数学(解析版) 题型:选择题
在公园的O处附近有E、F、G、H四棵树,位置如图所示(图中小正方形的边长均相等)现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E、F、G、H四棵树中需要被移除的为( )

A.E、F、G B.F、G、H C.G、H、E D.H、E、F
查看答案和解析>>
科目:初中数学 来源:2016年初中毕业升学考试(陕西卷)数学(解析版) 题型:解答题
某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶(500ml)、红茶(500ml)和可乐(600ml),抽奖规则如下:①如图,是一个材质均匀可自由转动的转盘,转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;②参与一次抽奖活动的顾客可进行两次“有效随机转动”(当转动转盘,转盘停止后,可获得指针所指区域的字样,我们称这次转动为一次“有效随机转动”);③假设顾客转动转盘,转盘停止后,指针指向两区域的边界,顾客可以再转动转盘,直到转动为一次“有效随机转动”;④当顾客完成一次抽奖活动后,记下两次指针所指区域的两个字,只要这两个字和奖品名称的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;不相同时,不能获得任何奖品.
根据以上规则,回答下列问题:

(1)求一次“有效随机转动”可获得“乐”字的概率;
(2)有一名顾客凭本超市的购物小票,参与了一次抽奖活动,请你用列表或树状图等方法,求该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率.
查看答案和解析>>
科目:初中数学 来源:2016年初中毕业升学考试(陕西卷)数学(解析版) 题型:单选题
设点A(a,b)是正比例函数y=﹣ x图象上的任意一点,则下列等式一定成立的是( )
x图象上的任意一点,则下列等式一定成立的是( )
A. 2a+3b=0 B. 2a﹣3b=0 C. 3a﹣2b=0 D. 3a+2b=0
查看答案和解析>>
科目:初中数学 来源:2016年初中毕业升学考试(山东东营卷)数学(解析版) 题型:解答题
如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y= 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=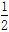 ,OB=4,OE=2.
,OB=4,OE=2.

(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果S△BAF=4S△DFO,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源:2016年初中毕业升学考试(山东东营卷)数学(解析版) 题型:填空题
某学习小组有8人,在一次数学测验中的成绩分别是:102,115,100,105,92,105,85,104,则他们成绩的平均数是_____________.
查看答案和解析>>
科目:初中数学 来源:2016年初中毕业升学考试(山东东营卷)数学(解析版) 题型:选择题
东营市某学校组织知识竞赛,共设有20道试题,其中有关中国优秀传统文化试题10道,实践应用试题6道,创新能力试题4道.小捷从中任选一道试题作答,他选中创新能力试题的概率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2016年初中毕业升学考试(辽宁大连卷)数学(解析版) 题型:解答题
阅读下面材料:
小明遇到这样一个问题:如图1,△ABC中,AB=AC,点D在BC边上,∠DAB=∠ABD,BE⊥AD,垂足为E,求证:BC=2AE.
小明经探究发现,过点A作AF⊥BC,垂足为F,得到∠AFB=∠BEA,从而可证△ABF≌△BAE(如图2),使问题得到解决.
(1)根据阅读材料回答:△ABF与△BAE全等的条件是 AAS(填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个)
参考小明思考问题的方法,解答下列问题:
(2)如图3,△ABC中,AB=AC,∠BAC=90°,D为BC的中点,E为DC的中点,点F在AC的延长线上,且∠CDF=∠EAC,若CF=2,求AB的长;
(3)如图4,△ABC中,AB=AC,∠BAC=120°,点D、E分别在AB、AC边上,且AD=kDB(其中0<k< ),∠AED=∠BCD,求
),∠AED=∠BCD,求 的值(用含k的式子表示).
的值(用含k的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com