
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对重庆市初中学生每天阅读时间的调查 | |
| B. | 对端午节期间市场上粽子质量情况的调查 | |
| C. | 对某批次手机的防水功能的调查 | |
| D. | 对某校九年级3班学生肺活量情况的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
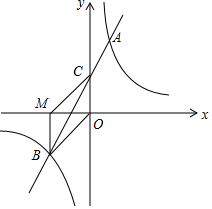 如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2$\sqrt{2}$,点A的纵坐标为4.
如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2$\sqrt{2}$,点A的纵坐标为4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
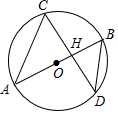 如图,AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB=$\frac{4}{5}$,BD=5,则OH的长度为( )
如图,AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB=$\frac{4}{5}$,BD=5,则OH的长度为( )| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{7}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com