
 k2
k2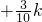 ;当k≥30时,y=0.02k,现经市场调查发现,在一个月中(按30天记数)有20天可卖出150份/天,有10天只能卖出100份/天,而报社规定每天批发给摊点的报纸的数量必须相同.
;当k≥30时,y=0.02k,现经市场调查发现,在一个月中(按30天记数)有20天可卖出150份/天,有10天只能卖出100份/天,而报社规定每天批发给摊点的报纸的数量必须相同. (x-100)2+
(x-100)2+ (x-100)]-0.3x×30,
(x-100)]-0.3x×30, x2+24x-800,
x2+24x-800, x2+24x-800,
x2+24x-800, (x-120)2+640,
(x-120)2+640,

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011年湖北省黄冈市中考数学模拟试卷(二)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com