D
分析:设GE=a,EF=b,AE=m,AB=c,Rt△EFG向右匀速运动的速度为1,分类讨论:当E点在点A左侧时,S=0,其图象为在x轴的线段;当点G在点A左侧,点E在点A右侧时,AE=t-m,GA=a-(t-m)=a+m-t,易证得△GAP∽△GEF,利用相似比可表示PA=

(a+m-t),S为图形PAEF的面积,则S=

[

(a+m-t)]•(t-m),可发现S是t的二次函数,且二次项系数为负数,所以抛物线开口向下;当点G在点A右侧,点E在点B左侧时,S为定值,定义三角形GEF的面积,其图象为平行于x轴的线段;当点G在点B左侧,点E在点B右侧时,和前面一样运用相似比可表示出PB=

(a+m+c-t),S为△GPB的面积,则S=

(t-a-m-c)
2,则S是t的二次函数,且二次项系数为,正数,所以抛物线开口向上.
解答:设GE=a,EF=b,AE=m,AB=c,Rt△EFG向右匀速运动的速度为1,
当E点在点A左侧时,S=0;
当点G在点A左侧,点E在点A右侧时,如图,
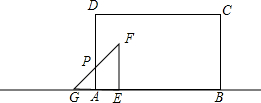
AE=t-m,GA=a-(t-m)=a+m-t,
∵PA∥EF,
∴△GAP∽△GEF,
∴
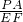
=
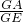
,即
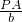
=
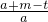
∴PA=

(a+m-t),
∴S=

(PA+FE)•AE=

[

(a+m-t)]•(t-m)
∴S是t的二次函数,且二次项系数为负数,所以抛物线开口向下;
当点G在点A右侧,点E在点B左侧时,S=

ab;
当点G在点B左侧,点E在点B右侧时,如图,
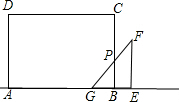
GB=a+m+c-t,
∵PA∥EF,
∴△GBP∽△GEF,
∴
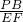
=
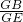
,
∴PB=

(a+m+c-t),
∴S=

GB•PB=

(a+m+c-t)•

(a+m+c-t)=

(t-a-m-c)
2,
∴S是t的二次函数,且二次项系数为,正数,所以抛物线开口向上,
综上所述,S与t的图象分为四段,第一段为x轴上的一条线段,第二段为开口向下的抛物线的一部分,第三段为与x轴平行的线段,第四段为开口向上的抛物线的一部分.
故选D.
点评:本题考查了动点问题的函数图象:先根据几何性质得到与动点有关的两变量之间的函数关系,然后利用函数解析式和函数性质画出其函数图象,注意自变量的取值范围.

 如图,点G、E、A、B在一条直线上,Rt△EFG从如图所示是位置出发,沿直线AB向右匀速运动,当点G与B重合时停止运动.设△EFG与矩形ABCD重合部分的面积为S,运动时间为t,则S与t的图象大致是
如图,点G、E、A、B在一条直线上,Rt△EFG从如图所示是位置出发,沿直线AB向右匀速运动,当点G与B重合时停止运动.设△EFG与矩形ABCD重合部分的面积为S,运动时间为t,则S与t的图象大致是



 (a+m-t),S为图形PAEF的面积,则S=
(a+m-t),S为图形PAEF的面积,则S= [
[ (a+m-t)]•(t-m),可发现S是t的二次函数,且二次项系数为负数,所以抛物线开口向下;当点G在点A右侧,点E在点B左侧时,S为定值,定义三角形GEF的面积,其图象为平行于x轴的线段;当点G在点B左侧,点E在点B右侧时,和前面一样运用相似比可表示出PB=
(a+m-t)]•(t-m),可发现S是t的二次函数,且二次项系数为负数,所以抛物线开口向下;当点G在点A右侧,点E在点B左侧时,S为定值,定义三角形GEF的面积,其图象为平行于x轴的线段;当点G在点B左侧,点E在点B右侧时,和前面一样运用相似比可表示出PB= (a+m+c-t),S为△GPB的面积,则S=
(a+m+c-t),S为△GPB的面积,则S= (t-a-m-c)2,则S是t的二次函数,且二次项系数为,正数,所以抛物线开口向上.
(t-a-m-c)2,则S是t的二次函数,且二次项系数为,正数,所以抛物线开口向上.
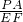 =
=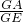 ,即
,即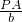 =
=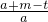
 (a+m-t),
(a+m-t), (PA+FE)•AE=
(PA+FE)•AE= [
[ (a+m-t)]•(t-m)
(a+m-t)]•(t-m) ab;
ab;
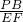 =
=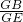 ,
, (a+m+c-t),
(a+m+c-t), GB•PB=
GB•PB= (a+m+c-t)•
(a+m+c-t)• (a+m+c-t)=
(a+m+c-t)= (t-a-m-c)2,
(t-a-m-c)2,

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°. 如图,点A的坐标为(2
如图,点A的坐标为(2