
分析 (1)根据总利润等于A、B两种型号时装的利润之和列式整理即可,再根据A、B两种时装所用甲、乙两种布料不超过现有布料列出不等式组求解即可;
(2)根据一次函数的增减性求出所获利润最大值即可.
解答 解:(1)y=30x+20(60-x)=10x+1200,
由题意$\left\{\begin{array}{l}{x+0.5(60-x)≤50}\\{0.2x+0.8(60-x)≤27}\end{array}\right.$,
解得35≤x≤40,
∵x是整数,
∴x=35,36,37,38,39,40
∴y=10x+1200(x=35,36,37,38,39,40)
(2)∵k=10>0,
∴y随x的增大而增大,
∴当x=40时,y有最大值为10×40+1200=1600,
答:当生产A型号的时装40套时,利润最大,最大利润为1600元.
点评 本题是贴近社会生活的应用题,赋予了生活气息,使学生真切地感受到“数学来源于生活”,体验到数学的“有用性”.这样设计体现了《新课程标准》的“问题情景-建立模型-解释、应用和拓展”的数学学习模式.


科目:初中数学 来源: 题型:选择题
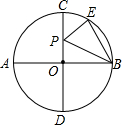 如图,AB、CD是⊙O的两条直径,且AB⊥CD,$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$,P为直径CD上一动点,若⊙O的直径AB=2,则△PEB周长的最小值是( )
如图,AB、CD是⊙O的两条直径,且AB⊥CD,$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$,P为直径CD上一动点,若⊙O的直径AB=2,则△PEB周长的最小值是( )| A. | 3 | B. | 4 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某互联网公司对用户实行两种收费方式:
某互联网公司对用户实行两种收费方式:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
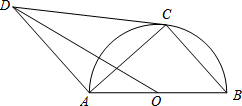 如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,AD∥BC,连接OD、AC.若tanB=$\frac{\sqrt{5}}{2}$,OD=3$\sqrt{6}$,则⊙O的半径为3.
如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,AD∥BC,连接OD、AC.若tanB=$\frac{\sqrt{5}}{2}$,OD=3$\sqrt{6}$,则⊙O的半径为3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com