已知四边形ABCD和对角线AC、BD,顺次连接各边中点得四边形MNPQ,给出以下6个命题:
①若所得四边形MNPQ为矩形,则原四边形ABCD为菱形;
②若所得四边形MNPQ为菱形,则原四边形ABCD为矩形;
③若所得四边形MNPQ为矩形,则AC⊥BD;
④若所得四边形MNPQ为菱形,则AC=BD;
⑤若所得四边形MNPQ为矩形,则∠BAD=90°;
⑥若所得四边形MNPQ为菱形,则AB=AD.以上命题中,正确的是( )
A.①②
B.③④
C.③④⑤⑥
D.①②③④
【答案】分析:根据三角形中位线定理,菱形的判定及矩形的判定对各个命题进行分析,从而可得到正确命题的个数.
解答:解:①若所得四边形MNPQ为矩形,原四边形ABCD只需满足对角线互相垂直即可,不一定是菱形,故①错误;
②若所得四边形MNPQ为菱形,则原四边形ABCD只需满足对角线相等即可,可以为等腰梯形,不一定是矩形,故②错误;
③若所得四边形MNPQ为矩形,则AC⊥BD,正确;
④若所得四边形MNPQ为菱形,则AC=BD,正确;
⑤若所得四边形MNPQ为矩形,则∠BAD=90°,错误;
⑥若所得四边形MNPQ为菱形,则AB=AD,错误.
综上可得只有③④正确;
故选B.
点评:此题主要考查三角形中位线定理,菱形的判定及矩形的判定的综合运用.



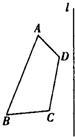 32、如图,已知四边形ABCD和直线L.
32、如图,已知四边形ABCD和直线L.