函数f(x)=x2+mx+m0(a,b∈R)的定义域为[-1,1],且|f(x)|的最大值为M.
(1)证明:|1+m0|≤M;
(2)求M的最小值,并求出当M取最小值时函数f(x)的解析式.
解:(1)证明:由已知:|f(-1)|=|1-m+m
0|≤M,|f(1)|=|1+m+m
0|≤M,
由公式:|(1-m+m
0)+(1+m+m
0)|≤|1-m+m
0|+|1+m+m
0|,
所以|2+2m
0|≤2M,
|1+m
0|≤M;
(2)∵f(0)=m
0,|f(0)|=|m
0|≤M,
∴|(1+m
0)-m
0|≤|1+m
0|+|m
0|≤2M,
∴M≥

.
∴M的最小值为

,
根据题意得出:1-m+m
0=

,1+m+m
0=

,
解得:
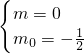
,
∴M取最小值时,函数f(x)的解析式为:y=x
2-

.
分析:(1)根据f(x)=x
2+mx+m
0(a,b∈R)的定义域为[-1,1],且|f(x)|的最大值为M,得出|f(-1)|=|1-m+m
0|≤M,|f(1)|=|1+m+m
0|≤M,进而得出|2+2m
0|≤2M,即可得出答案;
(2)利用f(0)=m
0,|f(0)|=|m
0|≤M,即可得出|(1+m
0)-m
0|≤|1+m
0|+|m
0|≤2M,再利用M取最小值求出函数f(x)的解析式.
点评:此题主要考查了函数定义域的性质,利用不等式的性质得出|(1-m+m
0)+(1+m+m
0)|≤|1-m+m
0|+|1+m+m
0|是解决问题的关键.

 .
. ,
, ,1+m+m0=
,1+m+m0= ,
,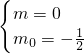 ,
, .
.

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案