
分析 将点的坐标代入二次函数解析式中可得出关于a、b、c的方程组,将其做差、整理后可得a=$\frac{1}{4-2b}$,再根据a<0即可求出b的取值范围.
解答 解:∵二次函数y=a(x-b)2+c(a<0)的图象经过点(1,1)和(3,3),
∴$\left\{\begin{array}{l}{1=a(1-b)^{2}+c①}\\{3=a(3-b)^{2}+c②}\end{array}\right.$,
②-①,整理得:a=$\frac{1}{4-2b}$.
∵a<0,
∴4-2b<0,
∴b>2.
故答案为:b>2.
点评 本题考查了二次函数图象上点的坐标特征,利用二次函数图象上点的坐标特征找出a=$\frac{1}{4-2b}$是解题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
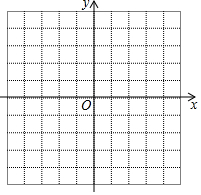 如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,建立如图所示的平面直角坐标系,已知点A(1,0),B(4,0),C(3,3),D(1,4)
如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,建立如图所示的平面直角坐标系,已知点A(1,0),B(4,0),C(3,3),D(1,4)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
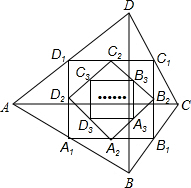 如图,四边形ABCD中,对角线AC⊥BD,且AC=2,BD=2,各边中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再各取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,以此类推,这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为21-n.
如图,四边形ABCD中,对角线AC⊥BD,且AC=2,BD=2,各边中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再各取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,以此类推,这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为21-n.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
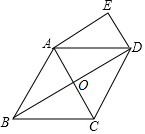 已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com