
【题目】如图1,把两个全等的三角板ABC、EFG叠放在一起,使三角板EFG的直角边FG经过三角板ABC的直角顶点C,垂直AB于G,其中∠B=∠F=30°,斜边AB和EF均为4.现将三角板EFG由图1所示的位置绕G点沿逆时针方向旋转α(0°<α<90°),如图2,EG交AC于点K,GF交BC于点H.在旋转过程中,请你解决以下问题:
(1)求证:△CGH∽△AGK;
(2)连接HK,求证:KH∥EF;
(3)设AK=x,△CKH的面积为y,求y关于x的函数关系式,并求出y的最大值.
【答案】
(1)
证明:在Rt△ABC中,CG⊥AB,∠B=30°,
∴∠GCH=∠GAK=60°,
又∠CGH=∠AGK=α,
∴△CGH∽△AGK;
(2)
证明:由(1)得△CGH∽△AGK,
∴ ![]() ;
;
在Rt△ACG中,tanA= ![]() =
= ![]() ,
,
∴ ![]() .
.
在Rt△KHG中,tan∠GKH= ![]() ,
,
∴∠GKH=60°.
∵Rt△EFG中,∠F=30°,
∴∠E=60°,
∴∠GKH=∠E,
∴KH∥EF;
(3)
解:由(1)得△CGH∽△AGK,
∴ ![]()
由(2)知 ![]() ,
,
∴ ![]() .
.
∴CH= ![]() AK=
AK= ![]() x,
x,
在Rt△ABC中,∠B=30°,
∴AC= ![]() AB=2,
AB=2,
∴CK=AC﹣AK=2﹣x,
∴y= ![]() CKCH=
CKCH= ![]() (2﹣x)
(2﹣x) ![]() x=﹣
x=﹣ ![]() x2+
x2+ ![]() x,
x,
又y═﹣ ![]() x2+
x2+ ![]() x=﹣
x=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
∴当x=1时,y有最大值为 ![]() .
.
【解析】(1)根据已知条件证明△AGK∽△CGH即可;(2)连接HK,由(1)可知在Rt△KHG中,tan∠GKH= ![]() ,所以∠GKH=60°,再根据三角形的内角和证明,∠E=∠EGF﹣∠F=90°﹣30°=60°,即可证得∠GKH=∠E=60°,利用同位角相等两线平行即可证明KH∥EF;(3)设AK=x,存在x=1,使△CKH的面积最大,由(1)得△AGK∽△CGH,所以CH=
,所以∠GKH=60°,再根据三角形的内角和证明,∠E=∠EGF﹣∠F=90°﹣30°=60°,即可证得∠GKH=∠E=60°,利用同位角相等两线平行即可证明KH∥EF;(3)设AK=x,存在x=1,使△CKH的面积最大,由(1)得△AGK∽△CGH,所以CH= ![]() AK=
AK= ![]() x,根据三角形的面积公式表示出S△CHK=
x,根据三角形的面积公式表示出S△CHK= ![]() CKCH=
CKCH= ![]() (2﹣x)
(2﹣x) ![]() x,再把二次函数的解析式化为顶点式即可求出x的值.
x,再把二次函数的解析式化为顶点式即可求出x的值.


科目:初中数学 来源: 题型:
【题目】今年4月23日,是第16个世界读书日.某校为了解学生每周课余自主阅读的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如图不完整的统计图表,请根据图表中的信息解答下列问题
组别 | 学习时间x(h) | 频数(人数) |
A | 0<x≤1 | 8 |
B | 1<x≤2 | 24 |
C | 2<x≤3 | 32 |
D | 3<x≤4 | n |
E | 4小时以上 | 4 |

(1)表中的n= , 中位数落在组,扇形统计图中B组对应的圆心角为°;
(2)请补全频数分布直方图;
(3)该校准备召开利用课余时间进行自主阅读的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB. 
(1)求证:PC是⊙O的切线;
(2)求证:BC= ![]() AB;
AB;
(3)点M是 ![]() 的中点,CM交AB于点N,若AB=4,求MNMC的值.
的中点,CM交AB于点N,若AB=4,求MNMC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题: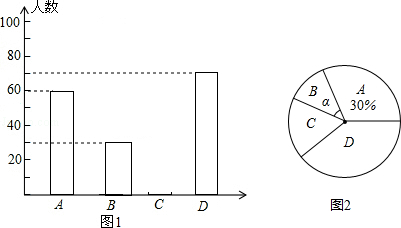
(1)本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)表示B等级的扇形圆心角α的度数是多少?
(4)在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,∠A=30°. 
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明)
(2)连接BD,求证:DE=CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com