
(本题6分)点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
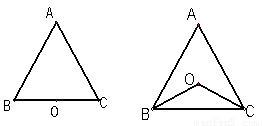
1.(1)如图1,若点O在边BC上,求证:AB=AC;
2.(2)如图2,若点O在△ABC的内部,求证:AB=AC;
3.(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.
1.(1)过点O分别作OE⊥AB,OF⊥AC,E、F分别是垂足,
由题意知,OE=OF,OB=OC,∴Rt△OEB≌Rt△OFC
∴∠B=∠C,从而AB=AC。
2. (2)过点O分别作OE⊥AB,OF⊥AC,EF分别是垂足,由
(2)过点O分别作OE⊥AB,OF⊥AC,EF分别是垂足,由
题意知,OE=OF。在Rt△OEB和Rt△OFC中,
∵OE=OF,OB=OC,∴Rt△OEB≌Rt△OFE。
∴∠OBE=∠OCF.
又由OB=OC知∠OBC=∠OCB,∴∠ABC=∠ACD,
∴AB=AC
3.(3)不一定成立。
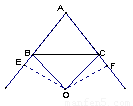
 (注:当∠A的平分线所在直线与边BC的垂直平分线重合时,有AB=AC;否则,AB≠AC,如示例图)画出不成立图得2分
(注:当∠A的平分线所在直线与边BC的垂直平分线重合时,有AB=AC;否则,AB≠AC,如示例图)画出不成立图得2分
【解析】略


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
| 13 |
| 13 |
| 13 |

查看答案和解析>>
科目:初中数学 来源: 题型:
(本题6分)点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.

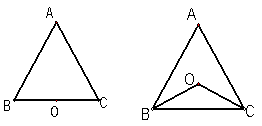
1.(1)如图1,若点O在边BC上,求证:AB=AC;
2.(2)如图2,若点O在△ABC的内部,求证:AB=AC;
3.(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012届浙江省温州乐清乐成公立寄宿学校八年级上学期期末考试数学卷 题型:解答题
(本题6分)点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.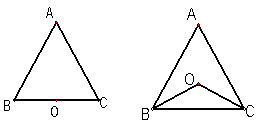
【小题1】(1)如图1,若点O在边BC上,求证:AB=AC;
【小题2】(2)如图2,若点O在△ABC的内部,求证:AB=AC;
【小题3】(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com