
科目:初中数学 来源:2016-2017学年湖北省武汉市侏儒山街四校七年级3月月考数学试卷(解析版) 题型:判断题
阅读理【解析】
计算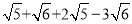 时我们可以将式子中的
时我们可以将式子中的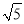 、
、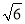 分别看成两个相同的字母a、b;则原式可看成a+b+2a﹣3b,我们用类比合并同类项的方法可将上面的式子化简.
分别看成两个相同的字母a、b;则原式可看成a+b+2a﹣3b,我们用类比合并同类项的方法可将上面的式子化简.
【解析】
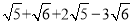
=(1+2)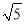 +(1-3)
+(1-3)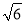
=3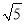 ﹣2
﹣2
类比以上解答方式化简: 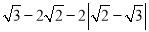 |
|
查看答案和解析>>
科目:初中数学 来源:2016-2017学年福建省泉州市泉港区七年级3月教学质量检测数学试卷(解析版) 题型:单选题
在解方程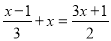 时,方程两边同时乘以6,去分母后,正确的是( )
时,方程两边同时乘以6,去分母后,正确的是( )
A. 2x﹣1+6x=3(3x+1) B. 2(x﹣1)+6x=3(3x+1)
C. 2(x﹣1)+x=3(3x+1) D. (x﹣1)+x=3(x+1)
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,由4个小正方形组成的田字格,△ABC的顶点都是小正方形的顶点,在田字格上能画出与△ABC成轴对称,且顶点都在小正方形顶点上的三角形的个数共有4个.
如图,由4个小正方形组成的田字格,△ABC的顶点都是小正方形的顶点,在田字格上能画出与△ABC成轴对称,且顶点都在小正方形顶点上的三角形的个数共有4个.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-4,0),B(2,0),与y轴交于点C(0,2).
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-4,0),B(2,0),与y轴交于点C(0,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com