
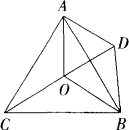
如图,已知△ABC为等边三角形,O为其内部一点,且∠OAC=∠DAB,AO=AD,连接OD,DB,已知AO=3 cm,BO=5 cm,CO=4 cm,求△ODB的周长.
|
由△ABC是等边三角形,得AC=AB,∠CAB=60°∴AC边以点A为旋转中心逆时针方向旋转60°之后得到AB边. 又∠OAC=∠DAB,∴∠OAD=∠OAB+∠DAB=∠CAB-∠OAC+∠DAB=∠CAB=60° 又AO=AD,∴OA边以点A为旋转中心,逆时针方旋转60°之后得到边AD. 从而可知△ADB是由△ACO绕点A逆时针方向旋转60°(∠BAC=60°)得到的.由旋转的特征,对应线段相等,且各点与中心的连线旋转了相同的角度,可得DB=OC,∠DAO=60°,又AO=AD,∴△AOD为正三角形,OD=AO, 故△ODB的周长为OD+DB+BO=AO+OC+BO=3+4+5=12(cm). ∴△ODB的周长为12 cm. |


科目:初中数学 来源: 题型:
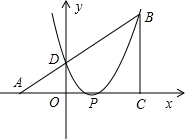 ,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图象经过点B、D.
,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图象经过点B、D.查看答案和解析>>
科目:初中数学 来源: 题型:
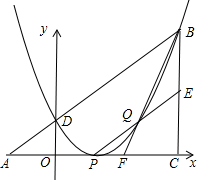 如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.
如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.查看答案和解析>>
科目:初中数学 来源: 题型:
 25、如图,已知△ABC为等边三角形,D、F分别为BC、AB边上的点,CD=BF,以AD为边作等边△ADE.
25、如图,已知△ABC为等边三角形,D、F分别为BC、AB边上的点,CD=BF,以AD为边作等边△ADE.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC为等边三角形,D,E,F分别在边BC,CA,AB上,且△DEF也是等边三角形,除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的.
如图,已知△ABC为等边三角形,D,E,F分别在边BC,CA,AB上,且△DEF也是等边三角形,除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC为等边三角形,点D.E分别在BC.AC边上,且AE=CD,AD与BE相交于点F.
如图,已知△ABC为等边三角形,点D.E分别在BC.AC边上,且AE=CD,AD与BE相交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com