Question

已知点P在线段4B上，点O在线段AB的延长线上，以点O为圆心，OP为半径作圆，点C是圆O上一点． 

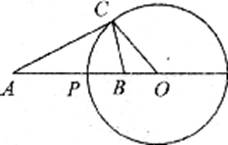
(1)如果AP=2PB，PB=BO．求证△CAO∽△BCO；

(2)如果AP=m(m是常数，且m>1)，BP=1，OP是OA、OB的比例中项，当点C在圆周上运动时，求AC：BC的值(结果用含m的式子表示)；

(3)在(2)的条件下，讨论以BC为半径的圆B和以CA为半径的圆C的位置关系，并写出相应的m的取值范围．

Answer 1

(1)证明：∵AP=2PB，PB=BO，∴AP=PO．

∴AO=2PO，

∵∴

∵∠COA=∠BOC，∴△CAO∽△BCO 

(2)解：设OP=x，则，．

∵OP是OA和OB的比例中项，

∴

解得．即  

∴．

∵OP是OA和OB的比例中项．即

∵OP=OC，∴

设圆O与线段AB的延长线相交于点Q，当点C、点P、点Q不重合时，

∵∠AOC=∠COB，∴△CAO∽△BCO．∴

∴当点C与点P或点Q重合时，可得

∴当点C在圆O上运动时，

 (3)解：由(2)得，AC>BC，且，   

，圆B和圆C的圆心距d=BC．

显然，，∴圆B和圆C的位置关系只能是相交、内切或内含．

当圆B与圆C相交时，，得．

∵,∴

当圆B与圆C内切时，．得m=2．

当圆口与圆C内含时，．得m>2．