
 ∠A(不必证明,本题可直接运用);在图②中,当BO′、CO′分别为∠ABC和∠ACB的外角平分线时,求∠BO′C与∠A的数量关系.我们可以利用“转化”的思想,将未知的∠BO′C转化为已知的∠BOC:如图②,作BO、CO平分∠ABC和∠ACB.
∠A(不必证明,本题可直接运用);在图②中,当BO′、CO′分别为∠ABC和∠ACB的外角平分线时,求∠BO′C与∠A的数量关系.我们可以利用“转化”的思想,将未知的∠BO′C转化为已知的∠BOC:如图②,作BO、CO平分∠ABC和∠ACB.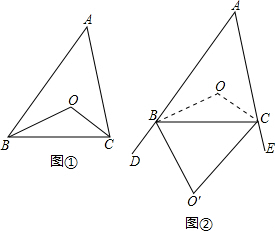
 ∠ABC,∠CBO′=
∠ABC,∠CBO′= ∠CBD,
∠CBD, (∠ABC+∠DBC)=90°;
(∠ABC+∠DBC)=90°;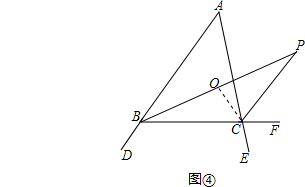
 ∠A.
∠A. ∠A.
∠A. ∠A.
∠A. ∠A,
∠A, ∠A.
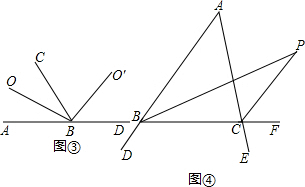
∠A. ∠A.由(1)中基本图形结论得:∠OBO′=∠OCO′=90°.根据四边形内角和是360度得到:∠OBO′+∠OCO′+∠BOC+∠BO′C=360°,则
∠A.由(1)中基本图形结论得:∠OBO′=∠OCO′=90°.根据四边形内角和是360度得到:∠OBO′+∠OCO′+∠BOC+∠BO′C=360°,则 ∠A.
∠A. ∠A.如图④,作CO平分∠ACB,交BP于点O.由(1)中基本图形结论得到:∠OCP=90°.利用∠BPC=90°+
∠A.如图④,作CO平分∠ACB,交BP于点O.由(1)中基本图形结论得到:∠OCP=90°.利用∠BPC=90°+ ∠A,故∠BPC=∠BOC-∠OCP=
∠A,故∠BPC=∠BOC-∠OCP= ∠A.
∠A.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
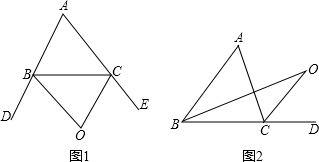 角平分线,若∠A=x°,求∠BOC的度数.
角平分线,若∠A=x°,求∠BOC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 角平分线,若∠A=x°,求∠BOC的度数.
角平分线,若∠A=x°,求∠BOC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com