
 已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=9没有实数根,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=9没有实数根,有下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据抛物线与x轴的交点个数对①进行判断;由抛物线开口方向得a<0,由抛物线的对称轴在y轴的右侧得b>0,由抛物线与y轴的交点在x轴上方得c>0,则可对②进行判断;由ax2+bx+c-m=0没有实数根得到抛物线y=ax2+bx+c与直线y=m没有公共点,加上二次函数的最大值为2,则m>2,于是可对③进行判断.
解答 解:∵抛物线与x轴有2个交点,
∴b2-4ac>0,故①正确;
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴的右侧,
∴b>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,故②正确;
∵ax2+bx+c-m=9没有实数根,
即抛物线y=ax2+bx+c与直线y=m+9没有公共点,
∵二次函数的最大值为2,
∴m>-7,故③错误.
故选:C.
点评 主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
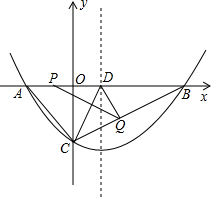 已知:抛物线y=$\frac{1}{16}$x2+bx+c(c<0)的图象与x轴的负半轴相较于点A,与x轴的正半轴相交于点B,与y轴交与点C,8OC2=3OA•OB且△ABC的面积为60.
已知:抛物线y=$\frac{1}{16}$x2+bx+c(c<0)的图象与x轴的负半轴相较于点A,与x轴的正半轴相交于点B,与y轴交与点C,8OC2=3OA•OB且△ABC的面积为60.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
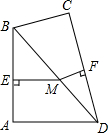 如图所示,在四边形ABCD中,∠A=∠C=90°,M为BD上任一点,ME⊥AB于E,MF⊥CD于F,求证:$\frac{MF}{BC}$+$\frac{ME}{AD}$=1.
如图所示,在四边形ABCD中,∠A=∠C=90°,M为BD上任一点,ME⊥AB于E,MF⊥CD于F,求证:$\frac{MF}{BC}$+$\frac{ME}{AD}$=1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
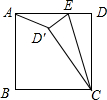 如图,正方形ABCD中,AB=4,E是边AD上一点,将△EDC沿EC翻折,点D的对应点D′落在正方形内部,若△AD′E恰是以D′E为腰的等腰三角形,那么DE的长为4$\sqrt{2}$-4或2.
如图,正方形ABCD中,AB=4,E是边AD上一点,将△EDC沿EC翻折,点D的对应点D′落在正方形内部,若△AD′E恰是以D′E为腰的等腰三角形,那么DE的长为4$\sqrt{2}$-4或2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在一次自行车越野赛中,出发mh后,小明骑行了25km,小刚骑行了18km,此后两人分别以akm/h,bkm/h匀速骑行,他们骑行的时间t(单位:h)与骑行的路程s(单位:km)之间的函数关系如图,观察图象,下列说法:
在一次自行车越野赛中,出发mh后,小明骑行了25km,小刚骑行了18km,此后两人分别以akm/h,bkm/h匀速骑行,他们骑行的时间t(单位:h)与骑行的路程s(单位:km)之间的函数关系如图,观察图象,下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com