


 ;
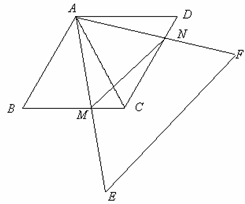
; /4×AM2,当AM最小时,S△AMN最小,即AM为BC边上的高,而AM=
/4×AM2,当AM最小时,S△AMN最小,即AM为BC边上的高,而AM= /2a,即可得到△AMN面积最小值。
/2a,即可得到△AMN面积最小值。 。
。 /4×AM2,
/4×AM2, /2a,
/2a, /4×3/4×a2=3
/4×3/4×a2=3 /16a2。
/16a2。

科目:初中数学 来源:不详 题型:单选题
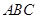 在平面直角坐标系中的位置如图所示,其中A(1, 2),B(1, 1),C(3, 1),将△
在平面直角坐标系中的位置如图所示,其中A(1, 2),B(1, 1),C(3, 1),将△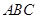 绕原点
绕原点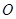 顺时针旋转
顺时针旋转 后得到△
后得到△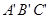 ,则点A旋转到点
,则点A旋转到点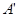 所经过的路线长为
所经过的路线长为
A. | B.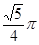 |
C.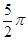 | D.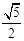 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 角(
角( ),当点A的对应点与点C重合时,B,C两点的对应点分别记为E,F,EF与AB的交点为G,此时
),当点A的对应点与点C重合时,B,C两点的对应点分别记为E,F,EF与AB的交点为G,此时 等于 ° ,△DEG的面积为 .
等于 ° ,△DEG的面积为 .
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
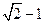 ,
,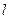 :
: 与坐标轴分别交于A、C两点,点B的坐标为(-4,1),⊙B与
与坐标轴分别交于A、C两点,点B的坐标为(-4,1),⊙B与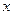

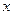 轴向右平移,同时,直线
轴向右平移,同时,直线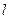 绕点A逆时针匀速旋转.当⊙B第一次与⊙O相切时,直线
绕点A逆时针匀速旋转.当⊙B第一次与⊙O相切时,直线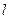 也恰好与⊙B第一次相切,问:直线
也恰好与⊙B第一次相切,问:直线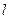 绕点A
绕点A 的值是否发生变化?如
的值是否发生变化?如
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com