
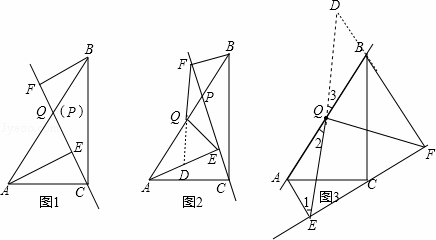
已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.

(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 AE∥BF ,QE与QF的数量关系式 QE=QF ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
考点:
全等三角形的判定与性质;直角三角形斜边上的中线.
分析:
(1)证△BFQ≌△AEQ即可;
(2)证△FBQ≌△DAQ,推出QF=QD,根据直角三角形斜边上中线性质求出即可;
(3)证△AEQ≌△BDQ,推出DQ=QE,根据直角三角形斜边上中线性质求出即可.
解答:
解:(1)AE∥BF,QE=QF,
理由是:如图1,∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴BF∥AE,∠BFQ=∠AEQ,
在△BFQ和△AEQ中
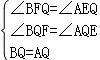
∴△BFQ≌△AEQ(AAS),
∴QE=QF,
故答案为:AE∥BF,QE=QF.
(2)QE=QF,
证明:如图2,延长FQ交AE于D,
∵AE∥BF,
∴∠QAD=∠FBQ,
在△FBQ和△DAQ中
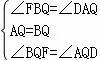
∴△FBQ≌△DAQ(ASA),
∴QF=QD,
∵AE⊥CP,
∴EQ是直角三角形DEF斜边上的中线,
∴QE=QF=QD,
即QE=QF.
(3)(2)中的结论仍然成立,
证明:如图3,
延长EQ、FB交于D,
∵AE∥BF,
∴∠1=∠D,
在△AQE和△BQD中
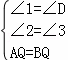 ,
,
∴△AQE≌△BQD(AAS),
∴QE=QD,
∵BF⊥CP,
∴FQ是斜边DE上的中线,
∴QE=QF.
点评:
本题考查了全等三角形的性质和判定,直角三角形斜边上中线性质的应用,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的性质是:全等三角形的对应边相等,对应角相等.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
| 3 |
| 2 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 :3.
:3. ,OC=8,OP=
,OC=8,OP= CQ.以矩形OABC的两边OA、OC所在的直线分别为x轴和y轴,建立平面直角坐标系,如图(3),若某抛物线顶点为P,点B在抛物线上.
CQ.以矩形OABC的两边OA、OC所在的直线分别为x轴和y轴,建立平面直角坐标系,如图(3),若某抛物线顶点为P,点B在抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
.如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角线APQ。当点P运动到原点O处时,记Q得位置为B。
(1)求点B的坐标;
(2)求证:当点P在x轴上运动(P不与Q重合)时,∠ABQ为定值;
(3)是否存在点P,使得以A、O、Q、B为顶点的四边形是梯形?若存在,请求出P点的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(湖北黄冈卷)数学 题型:解答题
.如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角线APQ。当点P运动到原点O处时,记Q得位置为B。
(1)求点B的坐标;
(2)求证:当点P在x轴上运动(P不与Q重合)时,∠ABQ为定值;
(3)是否存在点P,使得以A、O、Q、B为顶点的四边形是梯形?若存在,请求出P点的坐标;若不存在,请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com