
如图,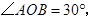 过
过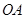 上到点
上到点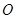 的距离为1,3,5,7,…的点作
的距离为1,3,5,7,…的点作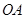 的垂线,分别与
的垂线,分别与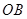 相交,得到图所示的阴影梯形,它们的面积依次记为
相交,得到图所示的阴影梯形,它们的面积依次记为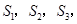 ….则
….则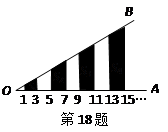
(1)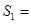 ;
;
(2)通过计算可得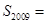 .
.
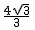 ,
, 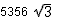
解析分析:(1)分析知奇数的通式为:2n-1(n为正整数),设阴影梯形的上底和下底距点O的长分别为a和b,则可以表达出Sn的表达式,将每个梯形的上底和下底距点O的长代入,求解即可;
(2)第2009个梯形前面已有2008×2个奇数,2009个梯形上底距点O的距离为第2008×2+1个奇数,下底为第2008×2+2个奇数.
解答:解:(1)设阴影梯形的上底和下底距点O的长分别为a和b,
则上底长为btan∠AOB,下底长为atan∠AOB,
∴Sn=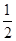 b×btan∠AOB-
b×btan∠AOB-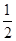 a×atan∠AOB=
a×atan∠AOB=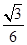 (b2-a2),
(b2-a2),
又∵梯形1距离点O的距离a=1,b=3,
∴S1=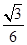 (32-12)=
(32-12)=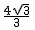 ;
;
(2)第2009个梯形前面已有2008×2个奇数,
2009个梯形上底距点O的距离为第2008×2+1个奇数,
下底为第2008×2+2个奇数,
∴第2009个梯形的两边长分别为:
a=2×(2008×2+1)-1=8033,
b=2×(2008×2+1)+1=8035,
故S2009=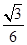 (80352-80332)=
(80352-80332)=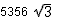 .
.
故答案为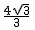 ,
, 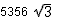 .
.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com