
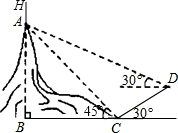
 如图,某电力项目中需要在一小山顶A处架一电线杆AH,使电线杆与小山的总高度BH为110米,测量时,工程人员王师傅在山脚下C点测得山顶A的仰角为45°,然后沿坡脚为30°的斜坡走40米到达D点,在D点测得山顶A的仰角为30°,求所需电线杆AH的高度(参考数据:
如图,某电力项目中需要在一小山顶A处架一电线杆AH,使电线杆与小山的总高度BH为110米,测量时,工程人员王师傅在山脚下C点测得山顶A的仰角为45°,然后沿坡脚为30°的斜坡走40米到达D点,在D点测得山顶A的仰角为30°,求所需电线杆AH的高度(参考数据: ≈1.73)
≈1.73)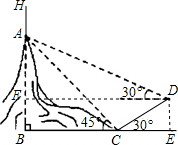


 ,
,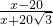 =
= ,
, )≈94.6(米),
)≈94.6(米),

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
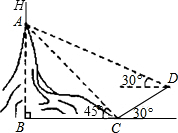 (2013•兰州一模)如图,某电力项目中需要在一小山顶A处架一电线杆AH,使电线杆与小山的总高度BH为110米,测量时,工程人员王师傅在山脚下C点测得山顶A的仰角为45°,然后沿坡脚为30°的斜坡走40米到达D点,在D点测得山顶A的仰角为30°,求所需电线杆AH的高度(参考数据:
(2013•兰州一模)如图,某电力项目中需要在一小山顶A处架一电线杆AH,使电线杆与小山的总高度BH为110米,测量时,工程人员王师傅在山脚下C点测得山顶A的仰角为45°,然后沿坡脚为30°的斜坡走40米到达D点,在D点测得山顶A的仰角为30°,求所需电线杆AH的高度(参考数据:| 3 |
查看答案和解析>>
科目:初中数学 来源:2013年甘肃省兰州市中考数学一模试卷(解析版) 题型:解答题
 ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com